Lumped capacitor#
The capacitance \(C\) of a system given a potential difference \(\Delta V\) between two conductors can be calculated from
\[ C = \frac{2W}{(\Delta V)^2} \]
with
\[ W = \frac{1}{2} \int_\Omega \epsilon E \cdot E d\Omega \]
where \(\epsilon\) is the permittivity distribution, \(E\) the electric field, and \(\Omega\) the domain. The integrand is only non-zero close to the conductors, where the field is concentrated.
In this notebook we compute the capacitance of a parallel-plate capacitor, and show that we recover the theoretical result \(C = \frac{\epsilon A}{d}\) in the limit of negligible fringe fields.
First, we parametrize a simple geometry:
import matplotlib.pyplot as plt
import numpy as np
import shapely
from meshwell.cad import cad
from meshwell.mesh import mesh
from meshwell.polysurface import PolySurface
from meshwell.resolution import ThresholdField
from skfem import Basis, ElementDG, ElementTriP0, Functional
from skfem.helpers import dot
from skfem.io.meshio import from_meshio
from femwell.coulomb import solve_coulomb
from femwell.visualization import plot_domains, plot_subdomain_boundaries
# Define some parameters for the capacitor:
dielectric_epsilon = 16
separation = 4
metal_thickness = 1
delta_voltage = 1
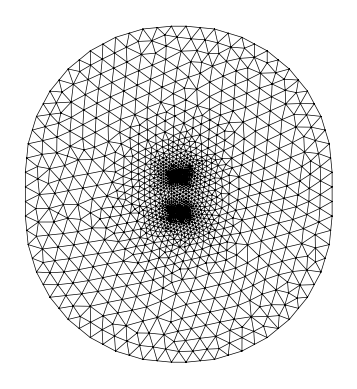
Make a mesh
Note: below we use meshwell instead of femwell's built-in backend. You can install meshwell with `pip install meshwell`
def parallel_plate_capacitor_mesh(
width,
separation=separation,
thickness=metal_thickness,
):
top_plate_polygon = shapely.geometry.box(
-width / 2, separation / 2, width / 2, separation / 2 + thickness
)
bottom_plate_polygon = shapely.geometry.box(
-width / 2, -separation / 2 - thickness, width / 2, -separation / 2
)
dielectric_polygon = shapely.geometry.box(
-width / 2, -separation / 2, width / 2, separation / 2
)
capacitor_polygon = shapely.unary_union(
[top_plate_polygon, bottom_plate_polygon, dielectric_polygon]
)
air_polygon = capacitor_polygon.buffer(20, resolution=8)
top_plate = PolySurface(
polygons=top_plate_polygon,
physical_name="top_plate",
mesh_bool=False,
mesh_order=1,
)
bottom_plate = PolySurface(
polygons=bottom_plate_polygon,
physical_name="bottom_plate",
mesh_bool=False,
mesh_order=2,
)
dielectric = PolySurface(
polygons=dielectric_polygon,
physical_name="dielectric",
mesh_bool=True,
mesh_order=3,
)
air = PolySurface(
polygons=air_polygon,
physical_name="air",
mesh_bool=True,
mesh_order=4,
)
cad(
entities_list=[top_plate, bottom_plate, dielectric, air],
output_file="/tmp/capacitor_example.xao",
)
mesh_output = mesh(
dim=3,
input_file="/tmp/capacitor_example.xao",
output_file="/tmp/capacitor_example.msh",
resolution_specs={
"top_plate": [ThresholdField(apply_to="curves", sizemin=0.2, distmax=10, sizemax=2)],
"bottom_plate": [ThresholdField(apply_to="curves", sizemin=0.2, distmax=10, sizemax=2)],
},
default_characteristic_length=2,
)
return from_meshio(mesh_output)
output_mesh = parallel_plate_capacitor_mesh(
width=2,
separation=separation,
thickness=metal_thickness,
)
output_mesh.draw().show()
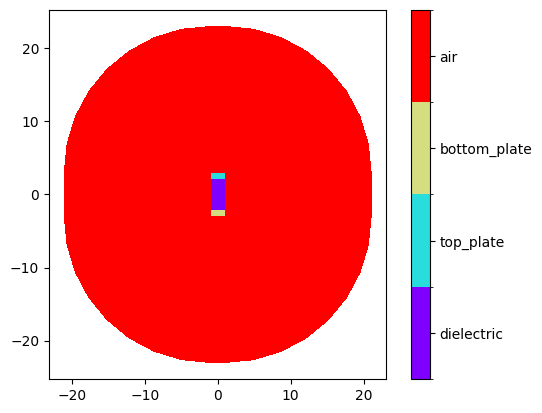
plot_domains(output_mesh)
plt.show()
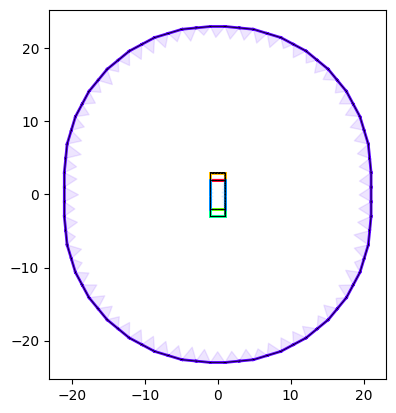
plot_subdomain_boundaries(output_mesh)
Show code cell output
Hide code cell output
Info : Clearing all models and views...
Info : Done clearing all models and views
Info : [ 0%] Difference
Info : [ 10%] Difference - Performing intersection of shapes
Info : [ 80%] Difference - Building splits of containers
Info : [ 0%] Fragments
Info : [ 10%] Fragments - Performing intersection of shapes
Info : [ 80%] Fragments - Building splits of containers
Info : [ 0%] Difference
Info : [ 10%] Difference
Info : [ 20%] Difference
Info : [ 30%] Difference
Info : [ 40%] Difference
Info : [ 50%] Difference
Info : [ 60%] Difference
Info : [ 70%] Difference
Info : [ 80%] Difference - Splitting faces
Info : [ 0%] Fragments
Info : [ 10%] Fragments
Info : [ 20%] Fragments
Info : [ 30%] Fragments
Info : [ 40%] Fragments
Info : [ 50%] Fragments
Info : [ 60%] Fragments
Info : [ 70%] Fragments
Info : [ 80%] Fragments - Splitting faces
Info : [ 0%] Difference
Info : [ 10%] Difference
Info : [ 20%] Difference
Info : [ 30%] Difference
Info : [ 40%] Difference
Info : [ 50%] Difference
Info : [ 60%] Difference
Info : [ 70%] Difference
Info : [ 80%] Difference - Making faces
Info : [ 90%] Difference - Adding holes
Info : [ 0%] Fragments
Info : [ 10%] Fragments
Info : [ 20%] Fragments
Info : [ 30%] Fragments
Info : [ 40%] Fragments
Info : [ 50%] Fragments
Info : [ 60%] Fragments
Info : [ 70%] Fragments
Info : [ 80%] Fragments - Splitting faces
Info : Writing '/tmp/capacitor_example.xao'...
Info : Done writing '/tmp/capacitor_example.xao'
Info : Clearing all models and views...
Info : Done clearing all models and views
Info : Reading '/tmp/capacitor_example.xao'...
Info : Done reading '/tmp/capacitor_example.xao'
<Axes: >
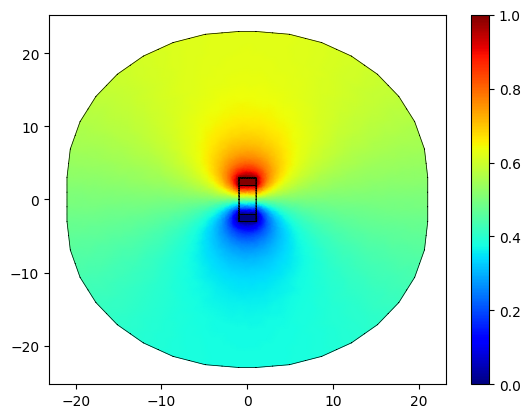
Since the electric field inside a metal is zero, we define the voltage on the boundary of the metal, and exclude the metal from the mesh:
def potential(input_mesh, dV=delta_voltage, dielectric_epsilon=16):
basis_epsilon = Basis(input_mesh, ElementTriP0())
epsilon = basis_epsilon.ones()
epsilon[basis_epsilon.get_dofs(elements=("dielectric"))] = dielectric_epsilon
basis_u, u = solve_coulomb(
basis_epsilon,
epsilon,
{
"top_plate___dielectric": dV,
"top_plate___air": dV,
"bottom_plate___dielectric": 0,
"bottom_plate___air": 0,
},
)
return basis_u, u, basis_epsilon, epsilon
basis_u, u, basis_epsilon, epsilon = potential(output_mesh, dV=delta_voltage)
fig, ax = plt.subplots()
for subdomain in basis_epsilon.mesh.subdomains.keys() - {"gmsh:bounding_entities"}:
basis_epsilon.mesh.restrict(subdomain).draw(ax=ax, boundaries_only=True)
basis_u.plot(u, ax=ax, shading="gouraud", colorbar=True)
# basis_vec.plot(-u_grad, ax=ax)
plt.show()
for subdomain in basis_epsilon.mesh.subdomains.keys() - {"gmsh:bounding_entities"}:
basis_epsilon.mesh.restrict(subdomain).draw(ax=ax, boundaries_only=True)
basis_grad = basis_u.with_element(ElementDG(basis_u.elem))
fig, ax = plt.subplots()
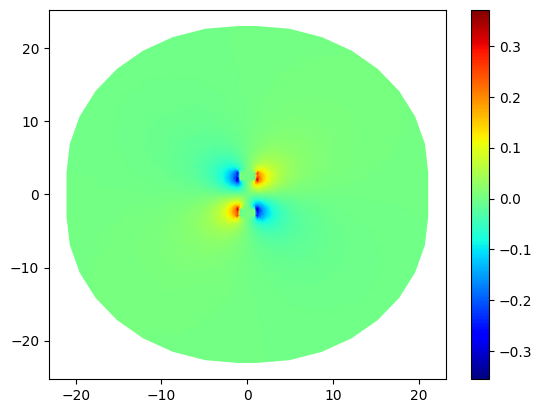
e_x = basis_u.project(-basis_epsilon.interpolate(epsilon) * basis_u.interpolate(u).grad[0])
basis_u.plot(e_x, ax=ax, shading="gouraud", colorbar=True)
plt.show()
fig, ax = plt.subplots()
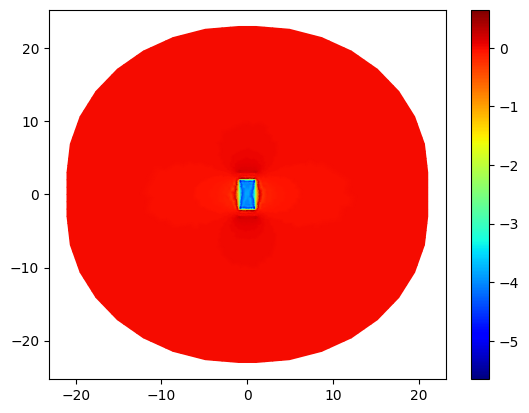
e_y = basis_u.project(-basis_epsilon.interpolate(epsilon) * basis_u.interpolate(u).grad[1])
basis_u.plot(e_y, ax=ax, shading="gouraud", colorbar=True)
plt.show()
def capacitance(
width=2,
separation=separation,
thickness=metal_thickness,
dV=delta_voltage,
dielectric_epsilon=dielectric_epsilon,
):
output_mesh = parallel_plate_capacitor_mesh(
width=width,
separation=separation,
thickness=thickness,
)
basis_u, u, basis_epsilon, epsilon = potential(
output_mesh, dV=dV, dielectric_epsilon=dielectric_epsilon
)
@Functional(dtype=complex)
def W(w):
return 0.5 * w["epsilon"] * dot(w["u"].grad, w["u"].grad)
C = (
2
* W.assemble(
basis_u,
epsilon=basis_epsilon.interpolate(epsilon),
u=basis_u.interpolate(u),
)
/ dV**2
)
return C
import tqdm
widths = np.linspace(1, 50, 21)
Cs_dict = {}
for dielectric_epsilon in [1, 3.9, 16]:
Cs = []
for width in tqdm.tqdm(widths):
Cs.append(
capacitance(
width=width,
separation=separation,
thickness=metal_thickness,
dV=delta_voltage,
dielectric_epsilon=dielectric_epsilon,
)
)
Cs_dict[dielectric_epsilon] = Cs
Show code cell output
Hide code cell output
Info : Clearing all models and views...
Info : Done clearing all models and views
Info : [ 0%] Difference
Info : [ 10%] Difference - Performing intersection of shapes
Info : [ 80%] Difference - Building splits of containers
Info : [ 0%] Fragments
Info : [ 10%] Fragments - Performing intersection of shapes
Info : [ 80%] Fragments - Building splits of containers
Info : [ 0%] Difference
Info : [ 10%] Difference
Info : [ 20%] Difference
Info : [ 30%] Difference
Info : [ 40%] Difference
Info : [ 50%] Difference
Info : [ 60%] Difference
Info : [ 70%] Difference
Info : [ 80%] Difference - Splitting faces
Info : [ 0%] Fragments
Info : [ 10%] Fragments
Info : [ 20%] Fragments
Info : [ 30%] Fragments
Info : [ 40%] Fragments
Info : [ 50%] Fragments
Info : [ 60%] Fragments
Info : [ 70%] Fragments
Info : [ 80%] Fragments - Splitting faces
Info : [ 0%] Difference
Info : [ 10%] Difference
Info : [ 20%] Difference
Info : [ 30%] Difference
Info : [ 40%] Difference
Info : [ 50%] Difference
Info : [ 60%] Difference
Info : [ 70%] Difference
Info : [ 80%] Difference - Making faces
Info : [ 90%] Difference - Adding holes
Info : [ 0%] Fragments
Info : [ 10%] Fragments
Info : [ 20%] Fragments
Info : [ 30%] Fragments
Info : [ 40%] Fragments
Info : [ 50%] Fragments
Info : [ 60%] Fragments
Info : [ 70%] Fragments
Info : [ 80%] Fragments - Splitting faces
Info : Writing '/tmp/capacitor_example.xao'...
Info : Done writing '/tmp/capacitor_example.xao'
Info : Clearing all models and views...
Info : Done clearing all models and views
Info : Reading '/tmp/capacitor_example.xao'...
Info : Done reading '/tmp/capacitor_example.xao'
Info : Clearing all models and views...
Info : Done clearing all models and views
Info : [ 0%] Difference
Info : [ 10%] Difference - Performing intersection of shapes
Info : [ 80%] Difference - Building splits of containers
Info : [ 0%] Fragments
Info : [ 10%] Fragments - Performing intersection of shapes
Info : [ 80%] Fragments - Building splits of containers
Info : [ 0%] Difference
Info : [ 10%] Difference
Info : [ 20%] Difference
Info : [ 30%] Difference
Info : [ 40%] Difference
Info : [ 50%] Difference
Info : [ 60%] Difference
Info : [ 70%] Difference
Info : [ 80%] Difference - Splitting faces
Info : [ 0%] Fragments
Info : [ 10%] Fragments
Info : [ 20%] Fragments
Info : [ 30%] Fragments
Info : [ 40%] Fragments
Info : [ 50%] Fragments
Info : [ 60%] Fragments
Info : [ 70%] Fragments
Info : [ 80%] Fragments - Splitting faces
Info : [ 0%] Difference
Info : [ 10%] Difference
Info : [ 20%] Difference
Info : [ 30%] Difference
Info : [ 40%] Difference
Info : [ 50%] Difference
Info : [ 60%] Difference
Info : [ 70%] Difference
Info : [ 80%] Difference - Making faces
Info : [ 90%] Difference - Adding holes
Info : [ 0%] Fragments
Info : [ 10%] Fragments
Info : [ 20%] Fragments
Info : [ 30%] Fragments
Info : [ 40%] Fragments
Info : [ 50%] Fragments
Info : [ 60%] Fragments
Info : [ 70%] Fragments
Info : [ 80%] Fragments - Splitting faces
Info : Writing '/tmp/capacitor_example.xao'...
Info : Done writing '/tmp/capacitor_example.xao'
Info : Clearing all models and views...
Info : Done clearing all models and views
Info : Reading '/tmp/capacitor_example.xao'...
Info : Done reading '/tmp/capacitor_example.xao'
Info : Clearing all models and views...
Info : Done clearing all models and views
Info : [ 0%] Difference
Info : [ 10%] Difference - Performing intersection of shapes
Info : [ 80%] Difference - Building splits of containers
Info : [ 0%] Fragments
Info : [ 10%] Fragments - Performing intersection of shapes
Info : [ 80%] Fragments - Building splits of containers
Info : [ 0%] Difference
Info : [ 10%] Difference
Info : [ 20%] Difference
Info : [ 30%] Difference
Info : [ 40%] Difference
Info : [ 50%] Difference
Info : [ 60%] Difference
Info : [ 70%] Difference
Info : [ 80%] Difference - Splitting faces
Info : [ 0%] Fragments
Info : [ 10%] Fragments
Info : [ 20%] Fragments
Info : [ 30%] Fragments
Info : [ 40%] Fragments
Info : [ 50%] Fragments
Info : [ 60%] Fragments
Info : [ 70%] Fragments
Info : [ 80%] Fragments - Splitting faces
Info : [ 0%] Difference
Info : [ 10%] Difference
Info : [ 20%] Difference
Info : [ 30%] Difference
Info : [ 40%] Difference
Info : [ 50%] Difference
Info : [ 60%] Difference
Info : [ 70%] Difference
Info : [ 80%] Difference - Making faces
Info : [ 90%] Difference - Adding holes
Info : [ 0%] Fragments
Info : [ 10%] Fragments
Info : [ 20%] Fragments
Info : [ 30%] Fragments
Info : [ 40%] Fragments
Info : [ 50%] Fragments
Info : [ 60%] Fragments
Info : [ 70%] Fragments
Info : [ 80%] Fragments - Splitting faces
Info : Writing '/tmp/capacitor_example.xao'...
Info : Done writing '/tmp/capacitor_example.xao'
Info : Clearing all models and views...
Info : Done clearing all models and views
Info : Reading '/tmp/capacitor_example.xao'...
Info : Done reading '/tmp/capacitor_example.xao'
Info : Clearing all models and views...
Info : Done clearing all models and views
Info : [ 0%] Difference
Info : [ 10%] Difference - Performing intersection of shapes
Info : [ 80%] Difference - Building splits of containers
Info : [ 0%] Fragments
Info : [ 10%] Fragments - Performing intersection of shapes
Info : [ 80%] Fragments - Building splits of containers
Info : [ 0%] Difference
Info : [ 10%] Difference
Info : [ 20%] Difference
Info : [ 30%] Difference
Info : [ 40%] Difference
Info : [ 50%] Difference
Info : [ 60%] Difference
Info : [ 70%] Difference
Info : [ 80%] Difference - Splitting faces
Info : [ 0%] Fragments
Info : [ 10%] Fragments
Info : [ 20%] Fragments
Info : [ 30%] Fragments
Info : [ 40%] Fragments
Info : [ 50%] Fragments
Info : [ 60%] Fragments
Info : [ 70%] Fragments
Info : [ 80%] Fragments - Splitting faces
Info : [ 0%] Difference
Info : [ 10%] Difference
Info : [ 20%] Difference
Info : [ 30%] Difference
Info : [ 40%] Difference
Info : [ 50%] Difference
Info : [ 60%] Difference
Info : [ 70%] Difference
Info : [ 80%] Difference - Making faces
Info : [ 90%] Difference - Adding holes
Info : [ 0%] Fragments
Info : [ 10%] Fragments
Info : [ 20%] Fragments
Info : [ 30%] Fragments
Info : [ 40%] Fragments
Info : [ 50%] Fragments
Info : [ 60%] Fragments
Info : [ 70%] Fragments
Info : [ 80%] Fragments - Splitting faces
Info : Writing '/tmp/capacitor_example.xao'...
Info : Done writing '/tmp/capacitor_example.xao'
Info : Clearing all models and views...
Info : Done clearing all models and views
Info : Reading '/tmp/capacitor_example.xao'...
Info : Done reading '/tmp/capacitor_example.xao'
Info : Clearing all models and views...
Info : Done clearing all models and views
Info : [ 0%] Difference
Info : [ 10%] Difference - Performing intersection of shapes
Info : [ 80%] Difference - Building splits of containers
Info : [ 0%] Fragments
Info : [ 10%] Fragments - Performing intersection of shapes
Info : [ 80%] Fragments - Building splits of containers
Info : [ 0%] Difference
Info : [ 10%] Difference
Info : [ 20%] Difference
Info : [ 30%] Difference
Info : [ 40%] Difference
Info : [ 50%] Difference
Info : [ 60%] Difference
Info : [ 70%] Difference
Info : [ 80%] Difference - Splitting faces
Info : [ 0%] Fragments
Info : [ 10%] Fragments
Info : [ 20%] Fragments
Info : [ 30%] Fragments
Info : [ 40%] Fragments
Info : [ 50%] Fragments
Info : [ 60%] Fragments
Info : [ 70%] Fragments
Info : [ 80%] Fragments - Splitting faces
Info : [ 0%] Difference
Info : [ 10%] Difference
Info : [ 20%] Difference
Info : [ 30%] Difference
Info : [ 40%] Difference
Info : [ 50%] Difference
Info : [ 60%] Difference
Info : [ 70%] Difference
Info : [ 80%] Difference - Making faces
Info : [ 90%] Difference - Adding holes
Info : [ 0%] Fragments
Info : [ 10%] Fragments
Info : [ 20%] Fragments
Info : [ 30%] Fragments
Info : [ 40%] Fragments
Info : [ 50%] Fragments
Info : [ 60%] Fragments
Info : [ 70%] Fragments
Info : [ 80%] Fragments - Splitting faces
Info : Writing '/tmp/capacitor_example.xao'...
Info : Done writing '/tmp/capacitor_example.xao'
Info : Clearing all models and views...
Info : Done clearing all models and views
Info : Reading '/tmp/capacitor_example.xao'...
Info : Done reading '/tmp/capacitor_example.xao'
Info : Clearing all models and views...
Info : Done clearing all models and views
Info : [ 0%] Difference
Info : [ 10%] Difference - Performing intersection of shapes
Info : [ 80%] Difference - Building splits of containers
Info : [ 0%] Fragments
Info : [ 10%] Fragments - Performing intersection of shapes
Info : [ 80%] Fragments - Building splits of containers
Info : [ 0%] Difference
Info : [ 10%] Difference
Info : [ 20%] Difference
Info : [ 30%] Difference
Info : [ 40%] Difference
Info : [ 50%] Difference
Info : [ 60%] Difference
Info : [ 70%] Difference
Info : [ 80%] Difference - Splitting faces
Info : [ 0%] Fragments
Info : [ 10%] Fragments
Info : [ 20%] Fragments
Info : [ 30%] Fragments
Info : [ 40%] Fragments
Info : [ 50%] Fragments
Info : [ 60%] Fragments
Info : [ 70%] Fragments
Info : [ 80%] Fragments - Splitting faces
Info : [ 0%] Difference
Info : [ 10%] Difference
Info : [ 20%] Difference
Info : [ 30%] Difference
Info : [ 40%] Difference
Info : [ 50%] Difference
Info : [ 60%] Difference
Info : [ 70%] Difference
Info : [ 80%] Difference - Making faces
Info : [ 90%] Difference - Adding holes
Info : [ 0%] Fragments
Info : [ 10%] Fragments
Info : [ 20%] Fragments
Info : [ 30%] Fragments
Info : [ 40%] Fragments
Info : [ 50%] Fragments
Info : [ 60%] Fragments
Info : [ 70%] Fragments
Info : [ 80%] Fragments - Splitting faces
Info : Writing '/tmp/capacitor_example.xao'...
Info : Done writing '/tmp/capacitor_example.xao'
Info : Clearing all models and views...
Info : Done clearing all models and views
Info : Reading '/tmp/capacitor_example.xao'...
Info : Done reading '/tmp/capacitor_example.xao'
Info : Clearing all models and views...
Info : Done clearing all models and views
Info : [ 0%] Difference
Info : [ 10%] Difference - Performing intersection of shapes
Info : [ 80%] Difference - Building splits of containers
Info : [ 0%] Fragments
Info : [ 10%] Fragments - Performing intersection of shapes
Info : [ 80%] Fragments - Building splits of containers
Info : [ 0%] Difference
Info : [ 10%] Difference
Info : [ 20%] Difference
Info : [ 30%] Difference
Info : [ 40%] Difference
Info : [ 50%] Difference
Info : [ 60%] Difference
Info : [ 70%] Difference
Info : [ 80%] Difference - Splitting faces
Info : [ 0%] Fragments
Info : [ 10%] Fragments
Info : [ 20%] Fragments
Info : [ 30%] Fragments
Info : [ 40%] Fragments
Info : [ 50%] Fragments
Info : [ 60%] Fragments
Info : [ 70%] Fragments
Info : [ 80%] Fragments - Splitting faces
Info : [ 0%] Difference
Info : [ 10%] Difference
Info : [ 20%] Difference
Info : [ 30%] Difference
Info : [ 40%] Difference
Info : [ 50%] Difference
Info : [ 60%] Difference
Info : [ 70%] Difference
Info : [ 80%] Difference - Making faces
Info : [ 90%] Difference - Adding holes
Info : [ 0%] Fragments
Info : [ 10%] Fragments
Info : [ 20%] Fragments
Info : [ 30%] Fragments
Info : [ 40%] Fragments
Info : [ 50%] Fragments
Info : [ 60%] Fragments
Info : [ 70%] Fragments
Info : [ 80%] Fragments - Splitting faces
Info : Writing '/tmp/capacitor_example.xao'...
Info : Done writing '/tmp/capacitor_example.xao'
Info : Clearing all models and views...
Info : Done clearing all models and views
Info : Reading '/tmp/capacitor_example.xao'...
Info : Done reading '/tmp/capacitor_example.xao'
Info : Clearing all models and views...
Info : Done clearing all models and views
Info : [ 0%] Difference
Info : [ 10%] Difference - Performing intersection of shapes
Info : [ 80%] Difference - Building splits of containers
Info : [ 0%] Fragments
Info : [ 10%] Fragments - Performing intersection of shapes
Info : [ 80%] Fragments - Building splits of containers
Info : [ 0%] Difference
Info : [ 10%] Difference
Info : [ 20%] Difference
Info : [ 30%] Difference
Info : [ 40%] Difference
Info : [ 50%] Difference
Info : [ 60%] Difference
Info : [ 70%] Difference
Info : [ 80%] Difference - Splitting faces
Info : [ 0%] Fragments
Info : [ 10%] Fragments
Info : [ 20%] Fragments
Info : [ 30%] Fragments
Info : [ 40%] Fragments
Info : [ 50%] Fragments
Info : [ 60%] Fragments
Info : [ 70%] Fragments
Info : [ 80%] Fragments - Splitting faces
Info : [ 0%] Difference
Info : [ 10%] Difference
Info : [ 20%] Difference
Info : [ 30%] Difference
Info : [ 40%] Difference
Info : [ 50%] Difference
Info : [ 60%] Difference
Info : [ 70%] Difference
Info : [ 80%] Difference - Making faces
Info : [ 90%] Difference - Adding holes
Info : [ 0%] Fragments
Info : [ 10%] Fragments
Info : [ 20%] Fragments
Info : [ 30%] Fragments
Info : [ 40%] Fragments
Info : [ 50%] Fragments
Info : [ 60%] Fragments
Info : [ 70%] Fragments
Info : [ 80%] Fragments - Splitting faces
Info : Writing '/tmp/capacitor_example.xao'...
Info : Done writing '/tmp/capacitor_example.xao'
Info : Clearing all models and views...
Info : Done clearing all models and views
Info : Reading '/tmp/capacitor_example.xao'...
Info : Done reading '/tmp/capacitor_example.xao'
Info : Clearing all models and views...
Info : Done clearing all models and views
Info : [ 0%] Difference
Info : [ 10%] Difference - Performing intersection of shapes
Info : [ 80%] Difference - Building splits of containers
Info : [ 0%] Fragments
Info : [ 10%] Fragments - Performing intersection of shapes
Info : [ 80%] Fragments - Building splits of containers
Info : [ 0%] Difference
Info : [ 10%] Difference
Info : [ 20%] Difference
Info : [ 30%] Difference
Info : [ 40%] Difference
Info : [ 50%] Difference
Info : [ 60%] Difference
Info : [ 70%] Difference
Info : [ 80%] Difference - Splitting faces
Info : [ 0%] Fragments
Info : [ 10%] Fragments
Info : [ 20%] Fragments
Info : [ 30%] Fragments
Info : [ 40%] Fragments
Info : [ 50%] Fragments
Info : [ 60%] Fragments
Info : [ 70%] Fragments
Info : [ 80%] Fragments - Splitting faces
Info : [ 0%] Difference
Info : [ 10%] Difference
Info : [ 20%] Difference
Info : [ 30%] Difference
Info : [ 40%] Difference
Info : [ 50%] Difference
Info : [ 60%] Difference
Info : [ 70%] Difference
Info : [ 80%] Difference - Making faces
Info : [ 90%] Difference - Adding holes
Info : [ 0%] Fragments
Info : [ 10%] Fragments
Info : [ 20%] Fragments
Info : [ 30%] Fragments
Info : [ 40%] Fragments
Info : [ 50%] Fragments
Info : [ 60%] Fragments
Info : [ 70%] Fragments
Info : [ 80%] Fragments - Splitting faces
Info : Writing '/tmp/capacitor_example.xao'...
Info : Done writing '/tmp/capacitor_example.xao'
Info : Clearing all models and views...
Info : Done clearing all models and views
Info : Reading '/tmp/capacitor_example.xao'...
Info : Done reading '/tmp/capacitor_example.xao'
Info : Clearing all models and views...
Info : Done clearing all models and views
Info : [ 0%] Difference
Info : [ 10%] Difference - Performing intersection of shapes
Info : [ 80%] Difference - Building splits of containers
Info : [ 0%] Fragments
Info : [ 10%] Fragments - Performing intersection of shapes
Info : [ 80%] Fragments - Building splits of containers
Info : [ 0%] Difference
Info : [ 10%] Difference
Info : [ 20%] Difference
Info : [ 30%] Difference
Info : [ 40%] Difference
Info : [ 50%] Difference
Info : [ 60%] Difference
Info : [ 70%] Difference
Info : [ 80%] Difference - Splitting faces
Info : [ 0%] Fragments
Info : [ 10%] Fragments
Info : [ 20%] Fragments
Info : [ 30%] Fragments
Info : [ 40%] Fragments
Info : [ 50%] Fragments
Info : [ 60%] Fragments
Info : [ 70%] Fragments
Info : [ 80%] Fragments - Splitting faces
Info : [ 0%] Difference
Info : [ 10%] Difference
Info : [ 20%] Difference
Info : [ 30%] Difference
Info : [ 40%] Difference
Info : [ 50%] Difference
Info : [ 60%] Difference
Info : [ 70%] Difference
Info : [ 80%] Difference - Making faces
Info : [ 90%] Difference - Adding holes
Info : [ 0%] Fragments
Info : [ 10%] Fragments
Info : [ 20%] Fragments
Info : [ 30%] Fragments
Info : [ 40%] Fragments
Info : [ 50%] Fragments
Info : [ 60%] Fragments
Info : [ 70%] Fragments
Info : [ 80%] Fragments - Splitting faces
Info : Writing '/tmp/capacitor_example.xao'...
Info : Done writing '/tmp/capacitor_example.xao'
Info : Clearing all models and views...
Info : Done clearing all models and views
Info : Reading '/tmp/capacitor_example.xao'...
Info : Done reading '/tmp/capacitor_example.xao'
Info : Clearing all models and views...
Info : Done clearing all models and views
Info : [ 0%] Difference
Info : [ 10%] Difference - Performing intersection of shapes
Info : [ 80%] Difference - Building splits of containers
Info : [ 0%] Fragments
Info : [ 10%] Fragments - Performing intersection of shapes
Info : [ 80%] Fragments - Building splits of containers
Info : [ 0%] Difference
Info : [ 10%] Difference
Info : [ 20%] Difference
Info : [ 30%] Difference
Info : [ 40%] Difference
Info : [ 50%] Difference
Info : [ 60%] Difference
Info : [ 70%] Difference
Info : [ 80%] Difference - Splitting faces
Info : [ 0%] Fragments
Info : [ 10%] Fragments
Info : [ 20%] Fragments
Info : [ 30%] Fragments
Info : [ 40%] Fragments
Info : [ 50%] Fragments
Info : [ 60%] Fragments
Info : [ 70%] Fragments
Info : [ 80%] Fragments - Splitting faces
Info : [ 0%] Difference
Info : [ 10%] Difference
Info : [ 20%] Difference
Info : [ 30%] Difference
Info : [ 40%] Difference
Info : [ 50%] Difference
Info : [ 60%] Difference
Info : [ 70%] Difference
Info : [ 80%] Difference - Making faces
Info : [ 90%] Difference - Adding holes
Info : [ 0%] Fragments
Info : [ 10%] Fragments
Info : [ 20%] Fragments
Info : [ 30%] Fragments
Info : [ 40%] Fragments
Info : [ 50%] Fragments
Info : [ 60%] Fragments
Info : [ 70%] Fragments
Info : [ 80%] Fragments - Splitting faces
Info : Writing '/tmp/capacitor_example.xao'...
Info : Done writing '/tmp/capacitor_example.xao'
Info : Clearing all models and views...
Info : Done clearing all models and views
Info : Reading '/tmp/capacitor_example.xao'...
Info : Done reading '/tmp/capacitor_example.xao'
Info : Clearing all models and views...
Info : Done clearing all models and views
Info : [ 0%] Difference
Info : [ 10%] Difference - Performing intersection of shapes
Info : [ 80%] Difference - Building splits of containers
Info : [ 0%] Fragments
Info : [ 10%] Fragments - Performing intersection of shapes
Info : [ 80%] Fragments - Building splits of containers
Info : [ 0%] Difference
Info : [ 10%] Difference
Info : [ 20%] Difference
Info : [ 30%] Difference
Info : [ 40%] Difference
Info : [ 50%] Difference
Info : [ 60%] Difference
Info : [ 70%] Difference
Info : [ 80%] Difference - Splitting faces
Info : [ 0%] Fragments
Info : [ 10%] Fragments
Info : [ 20%] Fragments
Info : [ 30%] Fragments
Info : [ 40%] Fragments
Info : [ 50%] Fragments
Info : [ 60%] Fragments
Info : [ 70%] Fragments
Info : [ 80%] Fragments - Splitting faces
Info : [ 0%] Difference
Info : [ 10%] Difference
Info : [ 20%] Difference
Info : [ 30%] Difference
Info : [ 40%] Difference
Info : [ 50%] Difference
Info : [ 60%] Difference
Info : [ 70%] Difference
Info : [ 80%] Difference - Making faces
Info : [ 90%] Difference - Adding holes
Info : [ 0%] Fragments
Info : [ 10%] Fragments
Info : [ 20%] Fragments
Info : [ 30%] Fragments
Info : [ 40%] Fragments
Info : [ 50%] Fragments
Info : [ 60%] Fragments
Info : [ 70%] Fragments
Info : [ 80%] Fragments - Splitting faces
Info : Writing '/tmp/capacitor_example.xao'...
Info : Done writing '/tmp/capacitor_example.xao'
Info : Clearing all models and views...
Info : Done clearing all models and views
Info : Reading '/tmp/capacitor_example.xao'...
Info : Done reading '/tmp/capacitor_example.xao'
Info : Clearing all models and views...
Info : Done clearing all models and views
Info : [ 0%] Difference
Info : [ 10%] Difference - Performing intersection of shapes
Info : [ 80%] Difference - Building splits of containers
Info : [ 0%] Fragments
Info : [ 10%] Fragments - Performing intersection of shapes
Info : [ 80%] Fragments - Building splits of containers
Info : [ 0%] Difference
Info : [ 10%] Difference
Info : [ 20%] Difference
Info : [ 30%] Difference
Info : [ 40%] Difference
Info : [ 50%] Difference
Info : [ 60%] Difference
Info : [ 70%] Difference
Info : [ 80%] Difference - Splitting faces
Info : [ 0%] Fragments
Info : [ 10%] Fragments
Info : [ 20%] Fragments
Info : [ 30%] Fragments
Info : [ 40%] Fragments
Info : [ 50%] Fragments
Info : [ 60%] Fragments
Info : [ 70%] Fragments
Info : [ 80%] Fragments - Splitting faces
Info : [ 0%] Difference
Info : [ 10%] Difference
Info : [ 20%] Difference
Info : [ 30%] Difference
Info : [ 40%] Difference
Info : [ 50%] Difference
Info : [ 60%] Difference
Info : [ 70%] Difference
Info : [ 80%] Difference - Making faces
Info : [ 90%] Difference - Adding holes
Info : [ 0%] Fragments
Info : [ 10%] Fragments
Info : [ 20%] Fragments
Info : [ 30%] Fragments
Info : [ 40%] Fragments
Info : [ 50%] Fragments
Info : [ 60%] Fragments
Info : [ 70%] Fragments
Info : [ 80%] Fragments - Splitting faces
Info : Writing '/tmp/capacitor_example.xao'...
Info : Done writing '/tmp/capacitor_example.xao'
Info : Clearing all models and views...
Info : Done clearing all models and views
Info : Reading '/tmp/capacitor_example.xao'...
Info : Done reading '/tmp/capacitor_example.xao'
Info : Clearing all models and views...
Info : Done clearing all models and views
Info : [ 0%] Difference
Info : [ 10%] Difference - Performing intersection of shapes
Info : [ 80%] Difference - Building splits of containers
Info : [ 0%] Fragments
Info : [ 10%] Fragments - Performing intersection of shapes
Info : [ 80%] Fragments - Building splits of containers
Info : [ 0%] Difference
Info : [ 10%] Difference
Info : [ 20%] Difference
Info : [ 30%] Difference
Info : [ 40%] Difference
Info : [ 50%] Difference
Info : [ 60%] Difference
Info : [ 70%] Difference
Info : [ 80%] Difference - Splitting faces
Info : [ 0%] Fragments
Info : [ 10%] Fragments
Info : [ 20%] Fragments
Info : [ 30%] Fragments
Info : [ 40%] Fragments
Info : [ 50%] Fragments
Info : [ 60%] Fragments
Info : [ 70%] Fragments
Info : [ 80%] Fragments - Splitting faces
Info : [ 0%] Difference
Info : [ 10%] Difference
Info : [ 20%] Difference
Info : [ 30%] Difference
Info : [ 40%] Difference
Info : [ 50%] Difference
Info : [ 60%] Difference
Info : [ 70%] Difference
Info : [ 80%] Difference - Making faces
Info : [ 90%] Difference - Adding holes
Info : [ 0%] Fragments
Info : [ 10%] Fragments
Info : [ 20%] Fragments
Info : [ 30%] Fragments
Info : [ 40%] Fragments
Info : [ 50%] Fragments
Info : [ 60%] Fragments
Info : [ 70%] Fragments
Info : [ 80%] Fragments - Splitting faces
Info : Writing '/tmp/capacitor_example.xao'...
Info : Done writing '/tmp/capacitor_example.xao'
Info : Clearing all models and views...
Info : Done clearing all models and views
Info : Reading '/tmp/capacitor_example.xao'...
Info : Done reading '/tmp/capacitor_example.xao'
Info : Clearing all models and views...
Info : Done clearing all models and views
Info : [ 0%] Difference
Info : [ 10%] Difference - Performing intersection of shapes
Info : [ 80%] Difference - Building splits of containers
Info : [ 0%] Fragments
Info : [ 10%] Fragments - Performing intersection of shapes
Info : [ 80%] Fragments - Building splits of containers
Info : [ 0%] Difference
Info : [ 10%] Difference
Info : [ 20%] Difference
Info : [ 30%] Difference
Info : [ 40%] Difference
Info : [ 50%] Difference
Info : [ 60%] Difference
Info : [ 70%] Difference
Info : [ 80%] Difference - Splitting faces
Info : [ 0%] Fragments
Info : [ 10%] Fragments
Info : [ 20%] Fragments
Info : [ 30%] Fragments
Info : [ 40%] Fragments
Info : [ 50%] Fragments
Info : [ 60%] Fragments
Info : [ 70%] Fragments
Info : [ 80%] Fragments - Splitting faces
Info : [ 0%] Difference
Info : [ 10%] Difference
Info : [ 20%] Difference
Info : [ 30%] Difference
Info : [ 40%] Difference
Info : [ 50%] Difference
Info : [ 60%] Difference
Info : [ 70%] Difference
Info : [ 80%] Difference - Making faces
Info : [ 90%] Difference - Adding holes
Info : [ 0%] Fragments
Info : [ 10%] Fragments
Info : [ 20%] Fragments
Info : [ 30%] Fragments
Info : [ 40%] Fragments
Info : [ 50%] Fragments
Info : [ 60%] Fragments
Info : [ 70%] Fragments
Info : [ 80%] Fragments - Splitting faces
Info : Writing '/tmp/capacitor_example.xao'...
Info : Done writing '/tmp/capacitor_example.xao'
Info : Clearing all models and views...
Info : Done clearing all models and views
Info : Reading '/tmp/capacitor_example.xao'...
Info : Done reading '/tmp/capacitor_example.xao'
Info : Clearing all models and views...
Info : Done clearing all models and views
Info : [ 0%] Difference
Info : [ 10%] Difference - Performing intersection of shapes
Info : [ 80%] Difference - Building splits of containers
Info : [ 0%] Fragments
Info : [ 10%] Fragments - Performing intersection of shapes
Info : [ 80%] Fragments - Building splits of containers
Info : [ 0%] Difference
Info : [ 10%] Difference
Info : [ 20%] Difference
Info : [ 30%] Difference
Info : [ 40%] Difference
Info : [ 50%] Difference
Info : [ 60%] Difference
Info : [ 70%] Difference
Info : [ 80%] Difference - Splitting faces
Info : [ 0%] Fragments
Info : [ 10%] Fragments
Info : [ 20%] Fragments
Info : [ 30%] Fragments
Info : [ 40%] Fragments
Info : [ 50%] Fragments
Info : [ 60%] Fragments
Info : [ 70%] Fragments
Info : [ 80%] Fragments - Splitting faces
Info : [ 0%] Difference
Info : [ 10%] Difference
Info : [ 20%] Difference
Info : [ 30%] Difference
Info : [ 40%] Difference
Info : [ 50%] Difference
Info : [ 60%] Difference
Info : [ 70%] Difference
Info : [ 80%] Difference - Making faces
Info : [ 90%] Difference - Adding holes
Info : [ 0%] Fragments
Info : [ 10%] Fragments
Info : [ 20%] Fragments
Info : [ 30%] Fragments
Info : [ 40%] Fragments
Info : [ 50%] Fragments
Info : [ 60%] Fragments
Info : [ 70%] Fragments
Info : [ 80%] Fragments - Splitting faces
Info : Writing '/tmp/capacitor_example.xao'...
Info : Done writing '/tmp/capacitor_example.xao'
Info : Clearing all models and views...
Info : Done clearing all models and views
Info : Reading '/tmp/capacitor_example.xao'...
Info : Done reading '/tmp/capacitor_example.xao'
Info : Clearing all models and views...
Info : Done clearing all models and views
Info : [ 0%] Difference
Info : [ 10%] Difference - Performing intersection of shapes
Info : [ 80%] Difference - Building splits of containers
Info : [ 0%] Fragments
Info : [ 10%] Fragments - Performing intersection of shapes
Info : [ 80%] Fragments - Building splits of containers
Info : [ 0%] Difference
Info : [ 10%] Difference
Info : [ 20%] Difference
Info : [ 30%] Difference
Info : [ 40%] Difference
Info : [ 50%] Difference
Info : [ 60%] Difference
Info : [ 70%] Difference
Info : [ 80%] Difference - Splitting faces
Info : [ 0%] Fragments
Info : [ 10%] Fragments
Info : [ 20%] Fragments
Info : [ 30%] Fragments
Info : [ 40%] Fragments
Info : [ 50%] Fragments
Info : [ 60%] Fragments
Info : [ 70%] Fragments
Info : [ 80%] Fragments - Splitting faces
Info : [ 0%] Difference
Info : [ 10%] Difference
Info : [ 20%] Difference
Info : [ 30%] Difference
Info : [ 40%] Difference
Info : [ 50%] Difference
Info : [ 60%] Difference
Info : [ 70%] Difference
Info : [ 80%] Difference - Making faces
Info : [ 90%] Difference - Adding holes
Info : [ 0%] Fragments
Info : [ 10%] Fragments
Info : [ 20%] Fragments
Info : [ 30%] Fragments
Info : [ 40%] Fragments
Info : [ 50%] Fragments
Info : [ 60%] Fragments
Info : [ 70%] Fragments
Info : [ 80%] Fragments - Splitting faces
Info : Writing '/tmp/capacitor_example.xao'...
Info : Done writing '/tmp/capacitor_example.xao'
Info : Clearing all models and views...
Info : Done clearing all models and views
Info : Reading '/tmp/capacitor_example.xao'...
Info : Done reading '/tmp/capacitor_example.xao'
Info : Clearing all models and views...
Info : Done clearing all models and views
Info : [ 0%] Difference
Info : [ 10%] Difference - Performing intersection of shapes
Info : [ 80%] Difference - Building splits of containers
Info : [ 0%] Fragments
Info : [ 10%] Fragments - Performing intersection of shapes
Info : [ 80%] Fragments - Building splits of containers
Info : [ 0%] Difference
Info : [ 10%] Difference
Info : [ 20%] Difference
Info : [ 30%] Difference
Info : [ 40%] Difference
Info : [ 50%] Difference
Info : [ 60%] Difference
Info : [ 70%] Difference
Info : [ 80%] Difference - Splitting faces
Info : [ 0%] Fragments
Info : [ 10%] Fragments
Info : [ 20%] Fragments
Info : [ 30%] Fragments
Info : [ 40%] Fragments
Info : [ 50%] Fragments
Info : [ 60%] Fragments
Info : [ 70%] Fragments
Info : [ 80%] Fragments - Splitting faces
Info : [ 0%] Difference
Info : [ 10%] Difference
Info : [ 20%] Difference
Info : [ 30%] Difference
Info : [ 40%] Difference
Info : [ 50%] Difference
Info : [ 60%] Difference
Info : [ 70%] Difference
Info : [ 80%] Difference - Making faces
Info : [ 90%] Difference - Adding holes
Info : [ 0%] Fragments
Info : [ 10%] Fragments
Info : [ 20%] Fragments
Info : [ 30%] Fragments
Info : [ 40%] Fragments
Info : [ 50%] Fragments
Info : [ 60%] Fragments
Info : [ 70%] Fragments
Info : [ 80%] Fragments - Splitting faces
Info : Writing '/tmp/capacitor_example.xao'...
Info : Done writing '/tmp/capacitor_example.xao'
Info : Clearing all models and views...
Info : Done clearing all models and views
Info : Reading '/tmp/capacitor_example.xao'...
Info : Done reading '/tmp/capacitor_example.xao'
Info : Clearing all models and views...
Info : Done clearing all models and views
Info : [ 0%] Difference
Info : [ 10%] Difference - Performing intersection of shapes
Info : [ 80%] Difference - Building splits of containers
Info : [ 0%] Fragments
Info : [ 10%] Fragments - Performing intersection of shapes
Info : [ 80%] Fragments - Building splits of containers
Info : [ 0%] Difference
Info : [ 10%] Difference
Info : [ 20%] Difference
Info : [ 30%] Difference
Info : [ 40%] Difference
Info : [ 50%] Difference
Info : [ 60%] Difference
Info : [ 70%] Difference
Info : [ 80%] Difference - Splitting faces
Info : [ 0%] Fragments
Info : [ 10%] Fragments
Info : [ 20%] Fragments
Info : [ 30%] Fragments
Info : [ 40%] Fragments
Info : [ 50%] Fragments
Info : [ 60%] Fragments
Info : [ 70%] Fragments
Info : [ 80%] Fragments - Splitting faces
Info : [ 0%] Difference
Info : [ 10%] Difference
Info : [ 20%] Difference
Info : [ 30%] Difference
Info : [ 40%] Difference
Info : [ 50%] Difference
Info : [ 60%] Difference
Info : [ 70%] Difference
Info : [ 80%] Difference - Making faces
Info : [ 90%] Difference - Adding holes
Info : [ 0%] Fragments
Info : [ 10%] Fragments
Info : [ 20%] Fragments
Info : [ 30%] Fragments
Info : [ 40%] Fragments
Info : [ 50%] Fragments
Info : [ 60%] Fragments
Info : [ 70%] Fragments
Info : [ 80%] Fragments - Splitting faces
Info : Writing '/tmp/capacitor_example.xao'...
Info : Done writing '/tmp/capacitor_example.xao'
Info : Clearing all models and views...
Info : Done clearing all models and views
Info : Reading '/tmp/capacitor_example.xao'...
Info : Done reading '/tmp/capacitor_example.xao'
Info : Clearing all models and views...
Info : Done clearing all models and views
Info : [ 0%] Difference
Info : [ 10%] Difference - Performing intersection of shapes
Info : [ 80%] Difference - Building splits of containers
Info : [ 0%] Fragments
Info : [ 10%] Fragments - Performing intersection of shapes
Info : [ 80%] Fragments - Building splits of containers
Info : [ 0%] Difference
Info : [ 10%] Difference
Info : [ 20%] Difference
Info : [ 30%] Difference
Info : [ 40%] Difference
Info : [ 50%] Difference
Info : [ 60%] Difference
Info : [ 70%] Difference
Info : [ 80%] Difference - Splitting faces
Info : [ 0%] Fragments
Info : [ 10%] Fragments
Info : [ 20%] Fragments
Info : [ 30%] Fragments
Info : [ 40%] Fragments
Info : [ 50%] Fragments
Info : [ 60%] Fragments
Info : [ 70%] Fragments
Info : [ 80%] Fragments - Splitting faces
Info : [ 0%] Difference
Info : [ 10%] Difference
Info : [ 20%] Difference
Info : [ 30%] Difference
Info : [ 40%] Difference
Info : [ 50%] Difference
Info : [ 60%] Difference
Info : [ 70%] Difference
Info : [ 80%] Difference - Making faces
Info : [ 90%] Difference - Adding holes
Info : [ 0%] Fragments
Info : [ 10%] Fragments
Info : [ 20%] Fragments
Info : [ 30%] Fragments
Info : [ 40%] Fragments
Info : [ 50%] Fragments
Info : [ 60%] Fragments
Info : [ 70%] Fragments
Info : [ 80%] Fragments - Splitting faces
Info : Writing '/tmp/capacitor_example.xao'...
Info : Done writing '/tmp/capacitor_example.xao'
Info : Clearing all models and views...
Info : Done clearing all models and views
Info : Reading '/tmp/capacitor_example.xao'...
Info : Done reading '/tmp/capacitor_example.xao'
Info : Clearing all models and views...
Info : Done clearing all models and views
Info : [ 0%] Difference
Info : [ 10%] Difference - Performing intersection of shapes
Info : [ 80%] Difference - Building splits of containers
Info : [ 0%] Fragments
Info : [ 10%] Fragments - Performing intersection of shapes
Info : [ 80%] Fragments - Building splits of containers
Info : [ 0%] Difference
Info : [ 10%] Difference
Info : [ 20%] Difference
Info : [ 30%] Difference
Info : [ 40%] Difference
Info : [ 50%] Difference
Info : [ 60%] Difference
Info : [ 70%] Difference
Info : [ 80%] Difference - Splitting faces
Info : [ 0%] Fragments
Info : [ 10%] Fragments
Info : [ 20%] Fragments
Info : [ 30%] Fragments
Info : [ 40%] Fragments
Info : [ 50%] Fragments
Info : [ 60%] Fragments
Info : [ 70%] Fragments
Info : [ 80%] Fragments - Splitting faces
Info : [ 0%] Difference
Info : [ 10%] Difference
Info : [ 20%] Difference
Info : [ 30%] Difference
Info : [ 40%] Difference
Info : [ 50%] Difference
Info : [ 60%] Difference
Info : [ 70%] Difference
Info : [ 80%] Difference - Making faces
Info : [ 90%] Difference - Adding holes
Info : [ 0%] Fragments
Info : [ 10%] Fragments
Info : [ 20%] Fragments
Info : [ 30%] Fragments
Info : [ 40%] Fragments
Info : [ 50%] Fragments
Info : [ 60%] Fragments
Info : [ 70%] Fragments
Info : [ 80%] Fragments - Splitting faces
Info : Writing '/tmp/capacitor_example.xao'...
Info : Done writing '/tmp/capacitor_example.xao'
Info : Clearing all models and views...
Info : Done clearing all models and views
Info : Reading '/tmp/capacitor_example.xao'...
Info : Done reading '/tmp/capacitor_example.xao'
Info : Clearing all models and views...
Info : Done clearing all models and views
Info : [ 0%] Difference
Info : [ 10%] Difference - Performing intersection of shapes
Info : [ 80%] Difference - Building splits of containers
Info : [ 0%] Fragments
Info : [ 10%] Fragments - Performing intersection of shapes
Info : [ 80%] Fragments - Building splits of containers
Info : [ 0%] Difference
Info : [ 10%] Difference
Info : [ 20%] Difference
Info : [ 30%] Difference
Info : [ 40%] Difference
Info : [ 50%] Difference
Info : [ 60%] Difference
Info : [ 70%] Difference
Info : [ 80%] Difference - Splitting faces
Info : [ 0%] Fragments
Info : [ 10%] Fragments
Info : [ 20%] Fragments
Info : [ 30%] Fragments
Info : [ 40%] Fragments
Info : [ 50%] Fragments
Info : [ 60%] Fragments
Info : [ 70%] Fragments
Info : [ 80%] Fragments - Splitting faces
Info : [ 0%] Difference
Info : [ 10%] Difference
Info : [ 20%] Difference
Info : [ 30%] Difference
Info : [ 40%] Difference
Info : [ 50%] Difference
Info : [ 60%] Difference
Info : [ 70%] Difference
Info : [ 80%] Difference - Making faces
Info : [ 90%] Difference - Adding holes
Info : [ 0%] Fragments
Info : [ 10%] Fragments
Info : [ 20%] Fragments
Info : [ 30%] Fragments
Info : [ 40%] Fragments
Info : [ 50%] Fragments
Info : [ 60%] Fragments
Info : [ 70%] Fragments
Info : [ 80%] Fragments - Splitting faces
Info : Writing '/tmp/capacitor_example.xao'...
Info : Done writing '/tmp/capacitor_example.xao'
Info : Clearing all models and views...
Info : Done clearing all models and views
Info : Reading '/tmp/capacitor_example.xao'...
Info : Done reading '/tmp/capacitor_example.xao'
Info : Clearing all models and views...
Info : Done clearing all models and views
Info : [ 0%] Difference
Info : [ 10%] Difference - Performing intersection of shapes
Info : [ 80%] Difference - Building splits of containers
Info : [ 0%] Fragments
Info : [ 10%] Fragments - Performing intersection of shapes
Info : [ 80%] Fragments - Building splits of containers
Info : [ 0%] Difference
Info : [ 10%] Difference
Info : [ 20%] Difference
Info : [ 30%] Difference
Info : [ 40%] Difference
Info : [ 50%] Difference
Info : [ 60%] Difference
Info : [ 70%] Difference
Info : [ 80%] Difference - Splitting faces
Info : [ 0%] Fragments
Info : [ 10%] Fragments
Info : [ 20%] Fragments
Info : [ 30%] Fragments
Info : [ 40%] Fragments
Info : [ 50%] Fragments
Info : [ 60%] Fragments
Info : [ 70%] Fragments
Info : [ 80%] Fragments - Splitting faces
Info : [ 0%] Difference
Info : [ 10%] Difference
Info : [ 20%] Difference
Info : [ 30%] Difference
Info : [ 40%] Difference
Info : [ 50%] Difference
Info : [ 60%] Difference
Info : [ 70%] Difference
Info : [ 80%] Difference - Making faces
Info : [ 90%] Difference - Adding holes
Info : [ 0%] Fragments
Info : [ 10%] Fragments
Info : [ 20%] Fragments
Info : [ 30%] Fragments
Info : [ 40%] Fragments
Info : [ 50%] Fragments
Info : [ 60%] Fragments
Info : [ 70%] Fragments
Info : [ 80%] Fragments - Splitting faces
Info : Writing '/tmp/capacitor_example.xao'...
Info : Done writing '/tmp/capacitor_example.xao'
Info : Clearing all models and views...
Info : Done clearing all models and views
Info : Reading '/tmp/capacitor_example.xao'...
Info : Done reading '/tmp/capacitor_example.xao'
Info : Clearing all models and views...
Info : Done clearing all models and views
Info : [ 0%] Difference
Info : [ 10%] Difference - Performing intersection of shapes
Info : [ 80%] Difference - Building splits of containers
Info : [ 0%] Fragments
Info : [ 10%] Fragments - Performing intersection of shapes
Info : [ 80%] Fragments - Building splits of containers
Info : [ 0%] Difference
Info : [ 10%] Difference
Info : [ 20%] Difference
Info : [ 30%] Difference
Info : [ 40%] Difference
Info : [ 50%] Difference
Info : [ 60%] Difference
Info : [ 70%] Difference
Info : [ 80%] Difference - Splitting faces
Info : [ 0%] Fragments
Info : [ 10%] Fragments
Info : [ 20%] Fragments
Info : [ 30%] Fragments
Info : [ 40%] Fragments
Info : [ 50%] Fragments
Info : [ 60%] Fragments
Info : [ 70%] Fragments
Info : [ 80%] Fragments - Splitting faces
Info : [ 0%] Difference
Info : [ 10%] Difference
Info : [ 20%] Difference
Info : [ 30%] Difference
Info : [ 40%] Difference
Info : [ 50%] Difference
Info : [ 60%] Difference
Info : [ 70%] Difference
Info : [ 80%] Difference - Making faces
Info : [ 90%] Difference - Adding holes
Info : [ 0%] Fragments
Info : [ 10%] Fragments
Info : [ 20%] Fragments
Info : [ 30%] Fragments
Info : [ 40%] Fragments
Info : [ 50%] Fragments
Info : [ 60%] Fragments
Info : [ 70%] Fragments
Info : [ 80%] Fragments - Splitting faces
Info : Writing '/tmp/capacitor_example.xao'...
Info : Done writing '/tmp/capacitor_example.xao'
Info : Clearing all models and views...
Info : Done clearing all models and views
Info : Reading '/tmp/capacitor_example.xao'...
Info : Done reading '/tmp/capacitor_example.xao'
Info : Clearing all models and views...
Info : Done clearing all models and views
Info : [ 0%] Difference
Info : [ 10%] Difference - Performing intersection of shapes
Info : [ 80%] Difference - Building splits of containers
Info : [ 0%] Fragments
Info : [ 10%] Fragments - Performing intersection of shapes
Info : [ 80%] Fragments - Building splits of containers
Info : [ 0%] Difference
Info : [ 10%] Difference
Info : [ 20%] Difference
Info : [ 30%] Difference
Info : [ 40%] Difference
Info : [ 50%] Difference
Info : [ 60%] Difference
Info : [ 70%] Difference
Info : [ 80%] Difference - Splitting faces
Info : [ 0%] Fragments
Info : [ 10%] Fragments
Info : [ 20%] Fragments
Info : [ 30%] Fragments
Info : [ 40%] Fragments
Info : [ 50%] Fragments
Info : [ 60%] Fragments
Info : [ 70%] Fragments
Info : [ 80%] Fragments - Splitting faces
Info : [ 0%] Difference
Info : [ 10%] Difference
Info : [ 20%] Difference
Info : [ 30%] Difference
Info : [ 40%] Difference
Info : [ 50%] Difference
Info : [ 60%] Difference
Info : [ 70%] Difference
Info : [ 80%] Difference - Making faces
Info : [ 90%] Difference - Adding holes
Info : [ 0%] Fragments
Info : [ 10%] Fragments
Info : [ 20%] Fragments
Info : [ 30%] Fragments
Info : [ 40%] Fragments
Info : [ 50%] Fragments
Info : [ 60%] Fragments
Info : [ 70%] Fragments
Info : [ 80%] Fragments - Splitting faces
Info : Writing '/tmp/capacitor_example.xao'...
Info : Done writing '/tmp/capacitor_example.xao'
Info : Clearing all models and views...
Info : Done clearing all models and views
Info : Reading '/tmp/capacitor_example.xao'...
Info : Done reading '/tmp/capacitor_example.xao'
Info : Clearing all models and views...
Info : Done clearing all models and views
Info : [ 0%] Difference
Info : [ 10%] Difference - Performing intersection of shapes
Info : [ 80%] Difference - Building splits of containers
Info : [ 0%] Fragments
Info : [ 10%] Fragments - Performing intersection of shapes
Info : [ 80%] Fragments - Building splits of containers
Info : [ 0%] Difference
Info : [ 10%] Difference
Info : [ 20%] Difference
Info : [ 30%] Difference
Info : [ 40%] Difference
Info : [ 50%] Difference
Info : [ 60%] Difference
Info : [ 70%] Difference
Info : [ 80%] Difference - Splitting faces
Info : [ 0%] Fragments
Info : [ 10%] Fragments
Info : [ 20%] Fragments
Info : [ 30%] Fragments
Info : [ 40%] Fragments
Info : [ 50%] Fragments
Info : [ 60%] Fragments
Info : [ 70%] Fragments
Info : [ 80%] Fragments - Splitting faces
Info : [ 0%] Difference
Info : [ 10%] Difference
Info : [ 20%] Difference
Info : [ 30%] Difference
Info : [ 40%] Difference
Info : [ 50%] Difference
Info : [ 60%] Difference
Info : [ 70%] Difference
Info : [ 80%] Difference - Making faces
Info : [ 90%] Difference - Adding holes
Info : [ 0%] Fragments
Info : [ 10%] Fragments
Info : [ 20%] Fragments
Info : [ 30%] Fragments
Info : [ 40%] Fragments
Info : [ 50%] Fragments
Info : [ 60%] Fragments
Info : [ 70%] Fragments
Info : [ 80%] Fragments - Splitting faces
Info : Writing '/tmp/capacitor_example.xao'...
Info : Done writing '/tmp/capacitor_example.xao'
Info : Clearing all models and views...
Info : Done clearing all models and views
Info : Reading '/tmp/capacitor_example.xao'...
Info : Done reading '/tmp/capacitor_example.xao'
Info : Clearing all models and views...
Info : Done clearing all models and views
Info : [ 0%] Difference
Info : [ 10%] Difference - Performing intersection of shapes
Info : [ 80%] Difference - Building splits of containers
Info : [ 0%] Fragments
Info : [ 10%] Fragments - Performing intersection of shapes
Info : [ 80%] Fragments - Building splits of containers
Info : [ 0%] Difference
Info : [ 10%] Difference
Info : [ 20%] Difference
Info : [ 30%] Difference
Info : [ 40%] Difference
Info : [ 50%] Difference
Info : [ 60%] Difference
Info : [ 70%] Difference
Info : [ 80%] Difference - Splitting faces
Info : [ 0%] Fragments
Info : [ 10%] Fragments
Info : [ 20%] Fragments
Info : [ 30%] Fragments
Info : [ 40%] Fragments
Info : [ 50%] Fragments
Info : [ 60%] Fragments
Info : [ 70%] Fragments
Info : [ 80%] Fragments - Splitting faces
Info : [ 0%] Difference
Info : [ 10%] Difference
Info : [ 20%] Difference
Info : [ 30%] Difference
Info : [ 40%] Difference
Info : [ 50%] Difference
Info : [ 60%] Difference
Info : [ 70%] Difference
Info : [ 80%] Difference - Making faces
Info : [ 90%] Difference - Adding holes
Info : [ 0%] Fragments
Info : [ 10%] Fragments
Info : [ 20%] Fragments
Info : [ 30%] Fragments
Info : [ 40%] Fragments
Info : [ 50%] Fragments
Info : [ 60%] Fragments
Info : [ 70%] Fragments
Info : [ 80%] Fragments - Splitting faces
Info : Writing '/tmp/capacitor_example.xao'...
Info : Done writing '/tmp/capacitor_example.xao'
Info : Clearing all models and views...
Info : Done clearing all models and views
Info : Reading '/tmp/capacitor_example.xao'...
Info : Done reading '/tmp/capacitor_example.xao'
Info : Clearing all models and views...
Info : Done clearing all models and views
Info : [ 0%] Difference
Info : [ 10%] Difference - Performing intersection of shapes
Info : [ 80%] Difference - Building splits of containers
Info : [ 0%] Fragments
Info : [ 10%] Fragments - Performing intersection of shapes
Info : [ 80%] Fragments - Building splits of containers
Info : [ 0%] Difference
Info : [ 10%] Difference
Info : [ 20%] Difference
Info : [ 30%] Difference
Info : [ 40%] Difference
Info : [ 50%] Difference
Info : [ 60%] Difference
Info : [ 70%] Difference
Info : [ 80%] Difference - Splitting faces
Info : [ 0%] Fragments
Info : [ 10%] Fragments
Info : [ 20%] Fragments
Info : [ 30%] Fragments
Info : [ 40%] Fragments
Info : [ 50%] Fragments
Info : [ 60%] Fragments
Info : [ 70%] Fragments
Info : [ 80%] Fragments - Splitting faces
Info : [ 0%] Difference
Info : [ 10%] Difference
Info : [ 20%] Difference
Info : [ 30%] Difference
Info : [ 40%] Difference
Info : [ 50%] Difference
Info : [ 60%] Difference
Info : [ 70%] Difference
Info : [ 80%] Difference - Making faces
Info : [ 90%] Difference - Adding holes
Info : [ 0%] Fragments
Info : [ 10%] Fragments
Info : [ 20%] Fragments
Info : [ 30%] Fragments
Info : [ 40%] Fragments
Info : [ 50%] Fragments
Info : [ 60%] Fragments
Info : [ 70%] Fragments
Info : [ 80%] Fragments - Splitting faces
Info : Writing '/tmp/capacitor_example.xao'...
Info : Done writing '/tmp/capacitor_example.xao'
Info : Clearing all models and views...
Info : Done clearing all models and views
Info : Reading '/tmp/capacitor_example.xao'...
Info : Done reading '/tmp/capacitor_example.xao'
Info : Clearing all models and views...
Info : Done clearing all models and views
Info : [ 0%] Difference
Info : [ 10%] Difference - Performing intersection of shapes
Info : [ 80%] Difference - Building splits of containers
Info : [ 0%] Fragments
Info : [ 10%] Fragments - Performing intersection of shapes
Info : [ 80%] Fragments - Building splits of containers
Info : [ 0%] Difference
Info : [ 10%] Difference
Info : [ 20%] Difference
Info : [ 30%] Difference
Info : [ 40%] Difference
Info : [ 50%] Difference
Info : [ 60%] Difference
Info : [ 70%] Difference
Info : [ 80%] Difference - Splitting faces
Info : [ 0%] Fragments
Info : [ 10%] Fragments
Info : [ 20%] Fragments
Info : [ 30%] Fragments
Info : [ 40%] Fragments
Info : [ 50%] Fragments
Info : [ 60%] Fragments
Info : [ 70%] Fragments
Info : [ 80%] Fragments - Splitting faces
Info : [ 0%] Difference
Info : [ 10%] Difference
Info : [ 20%] Difference
Info : [ 30%] Difference
Info : [ 40%] Difference
Info : [ 50%] Difference
Info : [ 60%] Difference
Info : [ 70%] Difference
Info : [ 80%] Difference - Making faces
Info : [ 90%] Difference - Adding holes
Info : [ 0%] Fragments
Info : [ 10%] Fragments
Info : [ 20%] Fragments
Info : [ 30%] Fragments
Info : [ 40%] Fragments
Info : [ 50%] Fragments
Info : [ 60%] Fragments
Info : [ 70%] Fragments
Info : [ 80%] Fragments - Splitting faces
Info : Writing '/tmp/capacitor_example.xao'...
Info : Done writing '/tmp/capacitor_example.xao'
Info : Clearing all models and views...
Info : Done clearing all models and views
Info : Reading '/tmp/capacitor_example.xao'...
Info : Done reading '/tmp/capacitor_example.xao'
Info : Clearing all models and views...
Info : Done clearing all models and views
Info : [ 0%] Difference
Info : [ 10%] Difference - Performing intersection of shapes
Info : [ 80%] Difference - Building splits of containers
Info : [ 0%] Fragments
Info : [ 10%] Fragments - Performing intersection of shapes
Info : [ 80%] Fragments - Building splits of containers
Info : [ 0%] Difference
Info : [ 10%] Difference
Info : [ 20%] Difference
Info : [ 30%] Difference
Info : [ 40%] Difference
Info : [ 50%] Difference
Info : [ 60%] Difference
Info : [ 70%] Difference
Info : [ 80%] Difference - Splitting faces
Info : [ 0%] Fragments
Info : [ 10%] Fragments
Info : [ 20%] Fragments
Info : [ 30%] Fragments
Info : [ 40%] Fragments
Info : [ 50%] Fragments
Info : [ 60%] Fragments
Info : [ 70%] Fragments
Info : [ 80%] Fragments - Splitting faces
Info : [ 0%] Difference
Info : [ 10%] Difference
Info : [ 20%] Difference
Info : [ 30%] Difference
Info : [ 40%] Difference
Info : [ 50%] Difference
Info : [ 60%] Difference
Info : [ 70%] Difference
Info : [ 80%] Difference - Making faces
Info : [ 90%] Difference - Adding holes
Info : [ 0%] Fragments
Info : [ 10%] Fragments
Info : [ 20%] Fragments
Info : [ 30%] Fragments
Info : [ 40%] Fragments
Info : [ 50%] Fragments
Info : [ 60%] Fragments
Info : [ 70%] Fragments
Info : [ 80%] Fragments - Splitting faces
Info : Writing '/tmp/capacitor_example.xao'...
Info : Done writing '/tmp/capacitor_example.xao'
Info : Clearing all models and views...
Info : Done clearing all models and views
Info : Reading '/tmp/capacitor_example.xao'...
Info : Done reading '/tmp/capacitor_example.xao'
Info : Clearing all models and views...
Info : Done clearing all models and views
Info : [ 0%] Difference
Info : [ 10%] Difference - Performing intersection of shapes
Info : [ 80%] Difference - Building splits of containers
Info : [ 0%] Fragments
Info : [ 10%] Fragments - Performing intersection of shapes
Info : [ 80%] Fragments - Building splits of containers
Info : [ 0%] Difference
Info : [ 10%] Difference
Info : [ 20%] Difference
Info : [ 30%] Difference
Info : [ 40%] Difference
Info : [ 50%] Difference
Info : [ 60%] Difference
Info : [ 70%] Difference
Info : [ 80%] Difference - Splitting faces
Info : [ 0%] Fragments
Info : [ 10%] Fragments
Info : [ 20%] Fragments
Info : [ 30%] Fragments
Info : [ 40%] Fragments
Info : [ 50%] Fragments
Info : [ 60%] Fragments
Info : [ 70%] Fragments
Info : [ 80%] Fragments - Splitting faces
Info : [ 0%] Difference
Info : [ 10%] Difference
Info : [ 20%] Difference
Info : [ 30%] Difference
Info : [ 40%] Difference
Info : [ 50%] Difference
Info : [ 60%] Difference
Info : [ 70%] Difference
Info : [ 80%] Difference - Making faces
Info : [ 90%] Difference - Adding holes
Info : [ 0%] Fragments
Info : [ 10%] Fragments
Info : [ 20%] Fragments
Info : [ 30%] Fragments
Info : [ 40%] Fragments
Info : [ 50%] Fragments
Info : [ 60%] Fragments
Info : [ 70%] Fragments
Info : [ 80%] Fragments - Splitting faces
Info : Writing '/tmp/capacitor_example.xao'...
Info : Done writing '/tmp/capacitor_example.xao'
Info : Clearing all models and views...
Info : Done clearing all models and views
Info : Reading '/tmp/capacitor_example.xao'...
Info : Done reading '/tmp/capacitor_example.xao'
Info : Clearing all models and views...
Info : Done clearing all models and views
Info : [ 0%] Difference
Info : [ 10%] Difference - Performing intersection of shapes
Info : [ 80%] Difference - Building splits of containers
Info : [ 0%] Fragments
Info : [ 10%] Fragments - Performing intersection of shapes
Info : [ 80%] Fragments - Building splits of containers
Info : [ 0%] Difference
Info : [ 10%] Difference
Info : [ 20%] Difference
Info : [ 30%] Difference
Info : [ 40%] Difference
Info : [ 50%] Difference
Info : [ 60%] Difference
Info : [ 70%] Difference
Info : [ 80%] Difference - Splitting faces
Info : [ 0%] Fragments
Info : [ 10%] Fragments
Info : [ 20%] Fragments
Info : [ 30%] Fragments
Info : [ 40%] Fragments
Info : [ 50%] Fragments
Info : [ 60%] Fragments
Info : [ 70%] Fragments
Info : [ 80%] Fragments - Splitting faces
Info : [ 0%] Difference
Info : [ 10%] Difference
Info : [ 20%] Difference
Info : [ 30%] Difference
Info : [ 40%] Difference
Info : [ 50%] Difference
Info : [ 60%] Difference
Info : [ 70%] Difference
Info : [ 80%] Difference - Making faces
Info : [ 90%] Difference - Adding holes
Info : [ 0%] Fragments
Info : [ 10%] Fragments
Info : [ 20%] Fragments
Info : [ 30%] Fragments
Info : [ 40%] Fragments
Info : [ 50%] Fragments
Info : [ 60%] Fragments
Info : [ 70%] Fragments
Info : [ 80%] Fragments - Splitting faces
Info : Writing '/tmp/capacitor_example.xao'...
Info : Done writing '/tmp/capacitor_example.xao'
Info : Clearing all models and views...
Info : Done clearing all models and views
Info : Reading '/tmp/capacitor_example.xao'...
Info : Done reading '/tmp/capacitor_example.xao'
Info : Clearing all models and views...
Info : Done clearing all models and views
Info : [ 0%] Difference
Info : [ 10%] Difference - Performing intersection of shapes
Info : [ 80%] Difference - Building splits of containers
Info : [ 0%] Fragments
Info : [ 10%] Fragments - Performing intersection of shapes
Info : [ 80%] Fragments - Building splits of containers
Info : [ 0%] Difference
Info : [ 10%] Difference
Info : [ 20%] Difference
Info : [ 30%] Difference
Info : [ 40%] Difference
Info : [ 50%] Difference
Info : [ 60%] Difference
Info : [ 70%] Difference
Info : [ 80%] Difference - Splitting faces
Info : [ 0%] Fragments
Info : [ 10%] Fragments
Info : [ 20%] Fragments
Info : [ 30%] Fragments
Info : [ 40%] Fragments
Info : [ 50%] Fragments
Info : [ 60%] Fragments
Info : [ 70%] Fragments
Info : [ 80%] Fragments - Splitting faces
Info : [ 0%] Difference
Info : [ 10%] Difference
Info : [ 20%] Difference
Info : [ 30%] Difference
Info : [ 40%] Difference
Info : [ 50%] Difference
Info : [ 60%] Difference
Info : [ 70%] Difference
Info : [ 80%] Difference - Making faces
Info : [ 90%] Difference - Adding holes
Info : [ 0%] Fragments
Info : [ 10%] Fragments
Info : [ 20%] Fragments
Info : [ 30%] Fragments
Info : [ 40%] Fragments
Info : [ 50%] Fragments
Info : [ 60%] Fragments
Info : [ 70%] Fragments
Info : [ 80%] Fragments - Splitting faces
Info : Writing '/tmp/capacitor_example.xao'...
Info : Done writing '/tmp/capacitor_example.xao'
Info : Clearing all models and views...
Info : Done clearing all models and views
Info : Reading '/tmp/capacitor_example.xao'...
Info : Done reading '/tmp/capacitor_example.xao'
Info : Clearing all models and views...
Info : Done clearing all models and views
Info : [ 0%] Difference
Info : [ 10%] Difference - Performing intersection of shapes
Info : [ 80%] Difference - Building splits of containers
Info : [ 0%] Fragments
Info : [ 10%] Fragments - Performing intersection of shapes
Info : [ 80%] Fragments - Building splits of containers
Info : [ 0%] Difference
Info : [ 10%] Difference
Info : [ 20%] Difference
Info : [ 30%] Difference
Info : [ 40%] Difference
Info : [ 50%] Difference
Info : [ 60%] Difference
Info : [ 70%] Difference
Info : [ 80%] Difference - Splitting faces
Info : [ 0%] Fragments
Info : [ 10%] Fragments
Info : [ 20%] Fragments
Info : [ 30%] Fragments
Info : [ 40%] Fragments
Info : [ 50%] Fragments
Info : [ 60%] Fragments
Info : [ 70%] Fragments
Info : [ 80%] Fragments - Splitting faces
Info : [ 0%] Difference
Info : [ 10%] Difference
Info : [ 20%] Difference
Info : [ 30%] Difference
Info : [ 40%] Difference
Info : [ 50%] Difference
Info : [ 60%] Difference
Info : [ 70%] Difference
Info : [ 80%] Difference - Making faces
Info : [ 90%] Difference - Adding holes
Info : [ 0%] Fragments
Info : [ 10%] Fragments
Info : [ 20%] Fragments
Info : [ 30%] Fragments
Info : [ 40%] Fragments
Info : [ 50%] Fragments
Info : [ 60%] Fragments
Info : [ 70%] Fragments
Info : [ 80%] Fragments - Splitting faces
Info : Writing '/tmp/capacitor_example.xao'...
Info : Done writing '/tmp/capacitor_example.xao'
Info : Clearing all models and views...
Info : Done clearing all models and views
Info : Reading '/tmp/capacitor_example.xao'...
Info : Done reading '/tmp/capacitor_example.xao'
Info : Clearing all models and views...
Info : Done clearing all models and views
Info : [ 0%] Difference
Info : [ 10%] Difference - Performing intersection of shapes
Info : [ 80%] Difference - Building splits of containers
Info : [ 0%] Fragments
Info : [ 10%] Fragments - Performing intersection of shapes
Info : [ 80%] Fragments - Building splits of containers
Info : [ 0%] Difference
Info : [ 10%] Difference
Info : [ 20%] Difference
Info : [ 30%] Difference
Info : [ 40%] Difference
Info : [ 50%] Difference
Info : [ 60%] Difference
Info : [ 70%] Difference
Info : [ 80%] Difference - Splitting faces
Info : [ 0%] Fragments
Info : [ 10%] Fragments
Info : [ 20%] Fragments
Info : [ 30%] Fragments
Info : [ 40%] Fragments
Info : [ 50%] Fragments
Info : [ 60%] Fragments
Info : [ 70%] Fragments
Info : [ 80%] Fragments - Splitting faces
Info : [ 0%] Difference
Info : [ 10%] Difference
Info : [ 20%] Difference
Info : [ 30%] Difference
Info : [ 40%] Difference
Info : [ 50%] Difference
Info : [ 60%] Difference
Info : [ 70%] Difference
Info : [ 80%] Difference - Making faces
Info : [ 90%] Difference - Adding holes
Info : [ 0%] Fragments
Info : [ 10%] Fragments
Info : [ 20%] Fragments
Info : [ 30%] Fragments
Info : [ 40%] Fragments
Info : [ 50%] Fragments
Info : [ 60%] Fragments
Info : [ 70%] Fragments
Info : [ 80%] Fragments - Splitting faces
Info : Writing '/tmp/capacitor_example.xao'...
Info : Done writing '/tmp/capacitor_example.xao'
Info : Clearing all models and views...
Info : Done clearing all models and views
Info : Reading '/tmp/capacitor_example.xao'...
Info : Done reading '/tmp/capacitor_example.xao'
Info : Clearing all models and views...
Info : Done clearing all models and views
Info : [ 0%] Difference
Info : [ 10%] Difference - Performing intersection of shapes
Info : [ 80%] Difference - Building splits of containers
Info : [ 0%] Fragments
Info : [ 10%] Fragments - Performing intersection of shapes
Info : [ 80%] Fragments - Building splits of containers
Info : [ 0%] Difference
Info : [ 10%] Difference
Info : [ 20%] Difference
Info : [ 30%] Difference
Info : [ 40%] Difference
Info : [ 50%] Difference
Info : [ 60%] Difference
Info : [ 70%] Difference
Info : [ 80%] Difference - Splitting faces
Info : [ 0%] Fragments
Info : [ 10%] Fragments
Info : [ 20%] Fragments
Info : [ 30%] Fragments
Info : [ 40%] Fragments
Info : [ 50%] Fragments
Info : [ 60%] Fragments
Info : [ 70%] Fragments
Info : [ 80%] Fragments - Splitting faces
Info : [ 0%] Difference
Info : [ 10%] Difference
Info : [ 20%] Difference
Info : [ 30%] Difference
Info : [ 40%] Difference
Info : [ 50%] Difference
Info : [ 60%] Difference
Info : [ 70%] Difference
Info : [ 80%] Difference - Making faces
Info : [ 90%] Difference - Adding holes
Info : [ 0%] Fragments
Info : [ 10%] Fragments
Info : [ 20%] Fragments
Info : [ 30%] Fragments
Info : [ 40%] Fragments
Info : [ 50%] Fragments
Info : [ 60%] Fragments
Info : [ 70%] Fragments
Info : [ 80%] Fragments - Splitting faces
Info : Writing '/tmp/capacitor_example.xao'...
Info : Done writing '/tmp/capacitor_example.xao'
Info : Clearing all models and views...
Info : Done clearing all models and views
Info : Reading '/tmp/capacitor_example.xao'...
Info : Done reading '/tmp/capacitor_example.xao'
Info : Clearing all models and views...
Info : Done clearing all models and views
Info : [ 0%] Difference
Info : [ 10%] Difference - Performing intersection of shapes
Info : [ 80%] Difference - Building splits of containers
Info : [ 0%] Fragments
Info : [ 10%] Fragments - Performing intersection of shapes
Info : [ 80%] Fragments - Building splits of containers
Info : [ 0%] Difference
Info : [ 10%] Difference
Info : [ 20%] Difference
Info : [ 30%] Difference
Info : [ 40%] Difference
Info : [ 50%] Difference
Info : [ 60%] Difference
Info : [ 70%] Difference
Info : [ 80%] Difference - Splitting faces
Info : [ 0%] Fragments
Info : [ 10%] Fragments
Info : [ 20%] Fragments
Info : [ 30%] Fragments
Info : [ 40%] Fragments
Info : [ 50%] Fragments
Info : [ 60%] Fragments
Info : [ 70%] Fragments
Info : [ 80%] Fragments - Splitting faces
Info : [ 0%] Difference
Info : [ 10%] Difference
Info : [ 20%] Difference
Info : [ 30%] Difference
Info : [ 40%] Difference
Info : [ 50%] Difference
Info : [ 60%] Difference
Info : [ 70%] Difference
Info : [ 80%] Difference - Making faces
Info : [ 90%] Difference - Adding holes
Info : [ 0%] Fragments
Info : [ 10%] Fragments
Info : [ 20%] Fragments
Info : [ 30%] Fragments
Info : [ 40%] Fragments
Info : [ 50%] Fragments
Info : [ 60%] Fragments
Info : [ 70%] Fragments
Info : [ 80%] Fragments - Splitting faces
Info : Writing '/tmp/capacitor_example.xao'...
Info : Done writing '/tmp/capacitor_example.xao'
Info : Clearing all models and views...
Info : Done clearing all models and views
Info : Reading '/tmp/capacitor_example.xao'...
Info : Done reading '/tmp/capacitor_example.xao'
Info : Clearing all models and views...
Info : Done clearing all models and views
Info : [ 0%] Difference
Info : [ 10%] Difference - Performing intersection of shapes
Info : [ 80%] Difference - Building splits of containers
Info : [ 0%] Fragments
Info : [ 10%] Fragments - Performing intersection of shapes
Info : [ 80%] Fragments - Building splits of containers
Info : [ 0%] Difference
Info : [ 10%] Difference
Info : [ 20%] Difference
Info : [ 30%] Difference
Info : [ 40%] Difference
Info : [ 50%] Difference
Info : [ 60%] Difference
Info : [ 70%] Difference
Info : [ 80%] Difference - Splitting faces
Info : [ 0%] Fragments
Info : [ 10%] Fragments
Info : [ 20%] Fragments
Info : [ 30%] Fragments
Info : [ 40%] Fragments
Info : [ 50%] Fragments
Info : [ 60%] Fragments
Info : [ 70%] Fragments
Info : [ 80%] Fragments - Splitting faces
Info : [ 0%] Difference
Info : [ 10%] Difference
Info : [ 20%] Difference
Info : [ 30%] Difference
Info : [ 40%] Difference
Info : [ 50%] Difference
Info : [ 60%] Difference
Info : [ 70%] Difference
Info : [ 80%] Difference - Making faces
Info : [ 90%] Difference - Adding holes
Info : [ 0%] Fragments
Info : [ 10%] Fragments
Info : [ 20%] Fragments
Info : [ 30%] Fragments
Info : [ 40%] Fragments
Info : [ 50%] Fragments
Info : [ 60%] Fragments
Info : [ 70%] Fragments
Info : [ 80%] Fragments - Splitting faces
Info : Writing '/tmp/capacitor_example.xao'...
Info : Done writing '/tmp/capacitor_example.xao'
Info : Clearing all models and views...
Info : Done clearing all models and views
Info : Reading '/tmp/capacitor_example.xao'...
Info : Done reading '/tmp/capacitor_example.xao'
Info : Clearing all models and views...
Info : Done clearing all models and views
Info : [ 0%] Difference
Info : [ 10%] Difference - Performing intersection of shapes
Info : [ 80%] Difference - Building splits of containers
Info : [ 0%] Fragments
Info : [ 10%] Fragments - Performing intersection of shapes
Info : [ 80%] Fragments - Building splits of containers
Info : [ 0%] Difference
Info : [ 10%] Difference
Info : [ 20%] Difference
Info : [ 30%] Difference
Info : [ 40%] Difference
Info : [ 50%] Difference
Info : [ 60%] Difference
Info : [ 70%] Difference
Info : [ 80%] Difference - Splitting faces
Info : [ 0%] Fragments
Info : [ 10%] Fragments
Info : [ 20%] Fragments
Info : [ 30%] Fragments
Info : [ 40%] Fragments
Info : [ 50%] Fragments
Info : [ 60%] Fragments
Info : [ 70%] Fragments
Info : [ 80%] Fragments - Splitting faces
Info : [ 0%] Difference
Info : [ 10%] Difference
Info : [ 20%] Difference
Info : [ 30%] Difference
Info : [ 40%] Difference
Info : [ 50%] Difference
Info : [ 60%] Difference
Info : [ 70%] Difference
Info : [ 80%] Difference - Making faces
Info : [ 90%] Difference - Adding holes
Info : [ 0%] Fragments
Info : [ 10%] Fragments
Info : [ 20%] Fragments
Info : [ 30%] Fragments
Info : [ 40%] Fragments
Info : [ 50%] Fragments
Info : [ 60%] Fragments
Info : [ 70%] Fragments
Info : [ 80%] Fragments - Splitting faces
Info : Writing '/tmp/capacitor_example.xao'...
Info : Done writing '/tmp/capacitor_example.xao'
Info : Clearing all models and views...
Info : Done clearing all models and views
Info : Reading '/tmp/capacitor_example.xao'...
Info : Done reading '/tmp/capacitor_example.xao'
Info : Clearing all models and views...
Info : Done clearing all models and views
Info : [ 0%] Difference
Info : [ 10%] Difference - Performing intersection of shapes
Info : [ 80%] Difference - Building splits of containers
Info : [ 0%] Fragments
Info : [ 10%] Fragments - Performing intersection of shapes
Info : [ 80%] Fragments - Building splits of containers
Info : [ 0%] Difference
Info : [ 10%] Difference
Info : [ 20%] Difference
Info : [ 30%] Difference
Info : [ 40%] Difference
Info : [ 50%] Difference
Info : [ 60%] Difference
Info : [ 70%] Difference
Info : [ 80%] Difference - Splitting faces
Info : [ 0%] Fragments
Info : [ 10%] Fragments
Info : [ 20%] Fragments
Info : [ 30%] Fragments
Info : [ 40%] Fragments
Info : [ 50%] Fragments
Info : [ 60%] Fragments
Info : [ 70%] Fragments
Info : [ 80%] Fragments - Splitting faces
Info : [ 0%] Difference
Info : [ 10%] Difference
Info : [ 20%] Difference
Info : [ 30%] Difference
Info : [ 40%] Difference
Info : [ 50%] Difference
Info : [ 60%] Difference
Info : [ 70%] Difference
Info : [ 80%] Difference - Making faces
Info : [ 90%] Difference - Adding holes
Info : [ 0%] Fragments
Info : [ 10%] Fragments
Info : [ 20%] Fragments
Info : [ 30%] Fragments
Info : [ 40%] Fragments
Info : [ 50%] Fragments
Info : [ 60%] Fragments
Info : [ 70%] Fragments
Info : [ 80%] Fragments - Splitting faces
Info : Writing '/tmp/capacitor_example.xao'...
Info : Done writing '/tmp/capacitor_example.xao'
Info : Clearing all models and views...
Info : Done clearing all models and views
Info : Reading '/tmp/capacitor_example.xao'...
Info : Done reading '/tmp/capacitor_example.xao'
Info : Clearing all models and views...
Info : Done clearing all models and views
Info : [ 0%] Difference
Info : [ 10%] Difference - Performing intersection of shapes
Info : [ 80%] Difference - Building splits of containers
Info : [ 0%] Fragments
Info : [ 10%] Fragments - Performing intersection of shapes
Info : [ 80%] Fragments - Building splits of containers
Info : [ 0%] Difference
Info : [ 10%] Difference
Info : [ 20%] Difference
Info : [ 30%] Difference
Info : [ 40%] Difference
Info : [ 50%] Difference
Info : [ 60%] Difference
Info : [ 70%] Difference
Info : [ 80%] Difference - Splitting faces
Info : [ 0%] Fragments
Info : [ 10%] Fragments
Info : [ 20%] Fragments
Info : [ 30%] Fragments
Info : [ 40%] Fragments
Info : [ 50%] Fragments
Info : [ 60%] Fragments
Info : [ 70%] Fragments
Info : [ 80%] Fragments - Splitting faces
Info : [ 0%] Difference
Info : [ 10%] Difference
Info : [ 20%] Difference
Info : [ 30%] Difference
Info : [ 40%] Difference
Info : [ 50%] Difference
Info : [ 60%] Difference
Info : [ 70%] Difference
Info : [ 80%] Difference - Making faces
Info : [ 90%] Difference - Adding holes
Info : [ 0%] Fragments
Info : [ 10%] Fragments
Info : [ 20%] Fragments
Info : [ 30%] Fragments
Info : [ 40%] Fragments
Info : [ 50%] Fragments
Info : [ 60%] Fragments
Info : [ 70%] Fragments
Info : [ 80%] Fragments - Splitting faces
Info : Writing '/tmp/capacitor_example.xao'...
Info : Done writing '/tmp/capacitor_example.xao'
Info : Clearing all models and views...
Info : Done clearing all models and views
Info : Reading '/tmp/capacitor_example.xao'...
Info : Done reading '/tmp/capacitor_example.xao'
Info : Clearing all models and views...
Info : Done clearing all models and views
Info : [ 0%] Difference
Info : [ 10%] Difference - Performing intersection of shapes
Info : [ 80%] Difference - Building splits of containers
Info : [ 0%] Fragments
Info : [ 10%] Fragments - Performing intersection of shapes
Info : [ 80%] Fragments - Building splits of containers
Info : [ 0%] Difference
Info : [ 10%] Difference
Info : [ 20%] Difference
Info : [ 30%] Difference
Info : [ 40%] Difference
Info : [ 50%] Difference
Info : [ 60%] Difference
Info : [ 70%] Difference
Info : [ 80%] Difference - Splitting faces
Info : [ 0%] Fragments
Info : [ 10%] Fragments
Info : [ 20%] Fragments
Info : [ 30%] Fragments
Info : [ 40%] Fragments
Info : [ 50%] Fragments
Info : [ 60%] Fragments
Info : [ 70%] Fragments
Info : [ 80%] Fragments - Splitting faces
Info : [ 0%] Difference
Info : [ 10%] Difference
Info : [ 20%] Difference
Info : [ 30%] Difference
Info : [ 40%] Difference
Info : [ 50%] Difference
Info : [ 60%] Difference
Info : [ 70%] Difference
Info : [ 80%] Difference - Making faces
Info : [ 90%] Difference - Adding holes
Info : [ 0%] Fragments
Info : [ 10%] Fragments
Info : [ 20%] Fragments
Info : [ 30%] Fragments
Info : [ 40%] Fragments
Info : [ 50%] Fragments
Info : [ 60%] Fragments
Info : [ 70%] Fragments
Info : [ 80%] Fragments - Splitting faces
Info : Writing '/tmp/capacitor_example.xao'...
Info : Done writing '/tmp/capacitor_example.xao'
Info : Clearing all models and views...
Info : Done clearing all models and views
Info : Reading '/tmp/capacitor_example.xao'...
Info : Done reading '/tmp/capacitor_example.xao'
Info : Clearing all models and views...
Info : Done clearing all models and views
Info : [ 0%] Difference
Info : [ 10%] Difference - Performing intersection of shapes
Info : [ 80%] Difference - Building splits of containers
Info : [ 0%] Fragments
Info : [ 10%] Fragments - Performing intersection of shapes
Info : [ 80%] Fragments - Building splits of containers
Info : [ 0%] Difference
Info : [ 10%] Difference
Info : [ 20%] Difference
Info : [ 30%] Difference
Info : [ 40%] Difference
Info : [ 50%] Difference
Info : [ 60%] Difference
Info : [ 70%] Difference
Info : [ 80%] Difference - Splitting faces
Info : [ 0%] Fragments
Info : [ 10%] Fragments
Info : [ 20%] Fragments
Info : [ 30%] Fragments
Info : [ 40%] Fragments
Info : [ 50%] Fragments
Info : [ 60%] Fragments
Info : [ 70%] Fragments
Info : [ 80%] Fragments - Splitting faces
Info : [ 0%] Difference
Info : [ 10%] Difference
Info : [ 20%] Difference
Info : [ 30%] Difference
Info : [ 40%] Difference
Info : [ 50%] Difference
Info : [ 60%] Difference
Info : [ 70%] Difference
Info : [ 80%] Difference - Making faces
Info : [ 90%] Difference - Adding holes
Info : [ 0%] Fragments
Info : [ 10%] Fragments
Info : [ 20%] Fragments
Info : [ 30%] Fragments
Info : [ 40%] Fragments
Info : [ 50%] Fragments
Info : [ 60%] Fragments
Info : [ 70%] Fragments
Info : [ 80%] Fragments - Splitting faces
Info : Writing '/tmp/capacitor_example.xao'...
Info : Done writing '/tmp/capacitor_example.xao'
Info : Clearing all models and views...
Info : Done clearing all models and views
Info : Reading '/tmp/capacitor_example.xao'...
Info : Done reading '/tmp/capacitor_example.xao'
Info : Clearing all models and views...
Info : Done clearing all models and views
Info : [ 0%] Difference
Info : [ 10%] Difference - Performing intersection of shapes
Info : [ 80%] Difference - Building splits of containers
Info : [ 0%] Fragments
Info : [ 10%] Fragments - Performing intersection of shapes
Info : [ 80%] Fragments - Building splits of containers
Info : [ 0%] Difference
Info : [ 10%] Difference
Info : [ 20%] Difference
Info : [ 30%] Difference
Info : [ 40%] Difference
Info : [ 50%] Difference
Info : [ 60%] Difference
Info : [ 70%] Difference
Info : [ 80%] Difference - Splitting faces
Info : [ 0%] Fragments
Info : [ 10%] Fragments
Info : [ 20%] Fragments
Info : [ 30%] Fragments
Info : [ 40%] Fragments
Info : [ 50%] Fragments
Info : [ 60%] Fragments
Info : [ 70%] Fragments
Info : [ 80%] Fragments - Splitting faces
Info : [ 0%] Difference
Info : [ 10%] Difference
Info : [ 20%] Difference
Info : [ 30%] Difference
Info : [ 40%] Difference
Info : [ 50%] Difference
Info : [ 60%] Difference
Info : [ 70%] Difference
Info : [ 80%] Difference - Making faces
Info : [ 90%] Difference - Adding holes
Info : [ 0%] Fragments
Info : [ 10%] Fragments
Info : [ 20%] Fragments
Info : [ 30%] Fragments
Info : [ 40%] Fragments
Info : [ 50%] Fragments
Info : [ 60%] Fragments
Info : [ 70%] Fragments
Info : [ 80%] Fragments - Splitting faces
Info : Writing '/tmp/capacitor_example.xao'...
Info : Done writing '/tmp/capacitor_example.xao'
Info : Clearing all models and views...
Info : Done clearing all models and views
Info : Reading '/tmp/capacitor_example.xao'...
Info : Done reading '/tmp/capacitor_example.xao'
Info : Clearing all models and views...
Info : Done clearing all models and views
Info : [ 0%] Difference
Info : [ 10%] Difference - Performing intersection of shapes
Info : [ 80%] Difference - Building splits of containers
Info : [ 0%] Fragments
Info : [ 10%] Fragments - Performing intersection of shapes
Info : [ 80%] Fragments - Building splits of containers
Info : [ 0%] Difference
Info : [ 10%] Difference
Info : [ 20%] Difference
Info : [ 30%] Difference
Info : [ 40%] Difference
Info : [ 50%] Difference
Info : [ 60%] Difference
Info : [ 70%] Difference
Info : [ 80%] Difference - Splitting faces
Info : [ 0%] Fragments
Info : [ 10%] Fragments
Info : [ 20%] Fragments
Info : [ 30%] Fragments
Info : [ 40%] Fragments
Info : [ 50%] Fragments
Info : [ 60%] Fragments
Info : [ 70%] Fragments
Info : [ 80%] Fragments - Splitting faces
Info : [ 0%] Difference
Info : [ 10%] Difference
Info : [ 20%] Difference
Info : [ 30%] Difference
Info : [ 40%] Difference
Info : [ 50%] Difference
Info : [ 60%] Difference
Info : [ 70%] Difference
Info : [ 80%] Difference - Making faces
Info : [ 90%] Difference - Adding holes
Info : [ 0%] Fragments
Info : [ 10%] Fragments
Info : [ 20%] Fragments
Info : [ 30%] Fragments
Info : [ 40%] Fragments
Info : [ 50%] Fragments
Info : [ 60%] Fragments
Info : [ 70%] Fragments
Info : [ 80%] Fragments - Splitting faces
Info : Writing '/tmp/capacitor_example.xao'...
Info : Done writing '/tmp/capacitor_example.xao'
Info : Clearing all models and views...
Info : Done clearing all models and views
Info : Reading '/tmp/capacitor_example.xao'...
Info : Done reading '/tmp/capacitor_example.xao'
Info : Clearing all models and views...
Info : Done clearing all models and views
Info : [ 0%] Difference
Info : [ 10%] Difference - Performing intersection of shapes
Info : [ 80%] Difference - Building splits of containers
Info : [ 0%] Fragments
Info : [ 10%] Fragments - Performing intersection of shapes
Info : [ 80%] Fragments - Building splits of containers
Info : [ 0%] Difference
Info : [ 10%] Difference
Info : [ 20%] Difference
Info : [ 30%] Difference
Info : [ 40%] Difference
Info : [ 50%] Difference
Info : [ 60%] Difference
Info : [ 70%] Difference
Info : [ 80%] Difference - Splitting faces
Info : [ 0%] Fragments
Info : [ 10%] Fragments
Info : [ 20%] Fragments
Info : [ 30%] Fragments
Info : [ 40%] Fragments
Info : [ 50%] Fragments
Info : [ 60%] Fragments
Info : [ 70%] Fragments
Info : [ 80%] Fragments - Splitting faces
Info : [ 0%] Difference
Info : [ 10%] Difference
Info : [ 20%] Difference
Info : [ 30%] Difference
Info : [ 40%] Difference
Info : [ 50%] Difference
Info : [ 60%] Difference
Info : [ 70%] Difference
Info : [ 80%] Difference - Making faces
Info : [ 90%] Difference - Adding holes
Info : [ 0%] Fragments
Info : [ 10%] Fragments
Info : [ 20%] Fragments
Info : [ 30%] Fragments
Info : [ 40%] Fragments
Info : [ 50%] Fragments
Info : [ 60%] Fragments
Info : [ 70%] Fragments
Info : [ 80%] Fragments - Splitting faces
Info : Writing '/tmp/capacitor_example.xao'...
Info : Done writing '/tmp/capacitor_example.xao'
Info : Clearing all models and views...
Info : Done clearing all models and views
Info : Reading '/tmp/capacitor_example.xao'...
Info : Done reading '/tmp/capacitor_example.xao'
Info : Clearing all models and views...
Info : Done clearing all models and views
Info : [ 0%] Difference
Info : [ 10%] Difference - Performing intersection of shapes
Info : [ 80%] Difference - Building splits of containers
Info : [ 0%] Fragments
Info : [ 10%] Fragments - Performing intersection of shapes
Info : [ 80%] Fragments - Building splits of containers
Info : [ 0%] Difference
Info : [ 10%] Difference
Info : [ 20%] Difference
Info : [ 30%] Difference
Info : [ 40%] Difference
Info : [ 50%] Difference
Info : [ 60%] Difference
Info : [ 70%] Difference
Info : [ 80%] Difference - Splitting faces
Info : [ 0%] Fragments
Info : [ 10%] Fragments
Info : [ 20%] Fragments
Info : [ 30%] Fragments
Info : [ 40%] Fragments
Info : [ 50%] Fragments
Info : [ 60%] Fragments
Info : [ 70%] Fragments
Info : [ 80%] Fragments - Splitting faces
Info : [ 0%] Difference
Info : [ 10%] Difference
Info : [ 20%] Difference
Info : [ 30%] Difference
Info : [ 40%] Difference
Info : [ 50%] Difference
Info : [ 60%] Difference
Info : [ 70%] Difference
Info : [ 80%] Difference - Making faces
Info : [ 90%] Difference - Adding holes
Info : [ 0%] Fragments
Info : [ 10%] Fragments
Info : [ 20%] Fragments
Info : [ 30%] Fragments
Info : [ 40%] Fragments
Info : [ 50%] Fragments
Info : [ 60%] Fragments
Info : [ 70%] Fragments
Info : [ 80%] Fragments - Splitting faces
Info : Writing '/tmp/capacitor_example.xao'...
Info : Done writing '/tmp/capacitor_example.xao'
Info : Clearing all models and views...
Info : Done clearing all models and views
Info : Reading '/tmp/capacitor_example.xao'...
Info : Done reading '/tmp/capacitor_example.xao'
Info : Clearing all models and views...
Info : Done clearing all models and views
Info : [ 0%] Difference
Info : [ 10%] Difference - Performing intersection of shapes
Info : [ 80%] Difference - Building splits of containers
Info : [ 0%] Fragments
Info : [ 10%] Fragments - Performing intersection of shapes
Info : [ 80%] Fragments - Building splits of containers
Info : [ 0%] Difference
Info : [ 10%] Difference
Info : [ 20%] Difference
Info : [ 30%] Difference
Info : [ 40%] Difference
Info : [ 50%] Difference
Info : [ 60%] Difference
Info : [ 70%] Difference
Info : [ 80%] Difference - Splitting faces
Info : [ 0%] Fragments
Info : [ 10%] Fragments
Info : [ 20%] Fragments
Info : [ 30%] Fragments
Info : [ 40%] Fragments
Info : [ 50%] Fragments
Info : [ 60%] Fragments
Info : [ 70%] Fragments
Info : [ 80%] Fragments - Splitting faces
Info : [ 0%] Difference
Info : [ 10%] Difference
Info : [ 20%] Difference
Info : [ 30%] Difference
Info : [ 40%] Difference
Info : [ 50%] Difference
Info : [ 60%] Difference
Info : [ 70%] Difference
Info : [ 80%] Difference - Making faces
Info : [ 90%] Difference - Adding holes
Info : [ 0%] Fragments
Info : [ 10%] Fragments
Info : [ 20%] Fragments
Info : [ 30%] Fragments
Info : [ 40%] Fragments
Info : [ 50%] Fragments
Info : [ 60%] Fragments
Info : [ 70%] Fragments
Info : [ 80%] Fragments - Splitting faces
Info : Writing '/tmp/capacitor_example.xao'...
Info : Done writing '/tmp/capacitor_example.xao'
Info : Clearing all models and views...
Info : Done clearing all models and views
Info : Reading '/tmp/capacitor_example.xao'...
Info : Done reading '/tmp/capacitor_example.xao'
Info : Clearing all models and views...
Info : Done clearing all models and views
Info : [ 0%] Difference
Info : [ 10%] Difference - Performing intersection of shapes
Info : [ 80%] Difference - Building splits of containers
Info : [ 0%] Fragments
Info : [ 10%] Fragments - Performing intersection of shapes
Info : [ 80%] Fragments - Building splits of containers
Info : [ 0%] Difference
Info : [ 10%] Difference
Info : [ 20%] Difference
Info : [ 30%] Difference
Info : [ 40%] Difference
Info : [ 50%] Difference
Info : [ 60%] Difference
Info : [ 70%] Difference
Info : [ 80%] Difference - Splitting faces
Info : [ 0%] Fragments
Info : [ 10%] Fragments
Info : [ 20%] Fragments
Info : [ 30%] Fragments
Info : [ 40%] Fragments
Info : [ 50%] Fragments
Info : [ 60%] Fragments
Info : [ 70%] Fragments
Info : [ 80%] Fragments - Splitting faces
Info : [ 0%] Difference
Info : [ 10%] Difference
Info : [ 20%] Difference
Info : [ 30%] Difference
Info : [ 40%] Difference
Info : [ 50%] Difference
Info : [ 60%] Difference
Info : [ 70%] Difference
Info : [ 80%] Difference - Making faces
Info : [ 90%] Difference - Adding holes
Info : [ 0%] Fragments
Info : [ 10%] Fragments
Info : [ 20%] Fragments
Info : [ 30%] Fragments
Info : [ 40%] Fragments
Info : [ 50%] Fragments
Info : [ 60%] Fragments
Info : [ 70%] Fragments
Info : [ 80%] Fragments - Splitting faces
Info : Writing '/tmp/capacitor_example.xao'...
Info : Done writing '/tmp/capacitor_example.xao'
Info : Clearing all models and views...
Info : Done clearing all models and views
Info : Reading '/tmp/capacitor_example.xao'...
Info : Done reading '/tmp/capacitor_example.xao'
Info : Clearing all models and views...
Info : Done clearing all models and views
Info : [ 0%] Difference
Info : [ 10%] Difference - Performing intersection of shapes
Info : [ 80%] Difference - Building splits of containers
Info : [ 0%] Fragments
Info : [ 10%] Fragments - Performing intersection of shapes
Info : [ 80%] Fragments - Building splits of containers
Info : [ 0%] Difference
Info : [ 10%] Difference
Info : [ 20%] Difference
Info : [ 30%] Difference
Info : [ 40%] Difference
Info : [ 50%] Difference
Info : [ 60%] Difference
Info : [ 70%] Difference
Info : [ 80%] Difference - Splitting faces
Info : [ 0%] Fragments
Info : [ 10%] Fragments
Info : [ 20%] Fragments
Info : [ 30%] Fragments
Info : [ 40%] Fragments
Info : [ 50%] Fragments
Info : [ 60%] Fragments
Info : [ 70%] Fragments
Info : [ 80%] Fragments - Splitting faces
Info : [ 0%] Difference
Info : [ 10%] Difference
Info : [ 20%] Difference
Info : [ 30%] Difference
Info : [ 40%] Difference
Info : [ 50%] Difference
Info : [ 60%] Difference
Info : [ 70%] Difference
Info : [ 80%] Difference - Making faces
Info : [ 90%] Difference - Adding holes
Info : [ 0%] Fragments
Info : [ 10%] Fragments
Info : [ 20%] Fragments
Info : [ 30%] Fragments
Info : [ 40%] Fragments
Info : [ 50%] Fragments
Info : [ 60%] Fragments
Info : [ 70%] Fragments
Info : [ 80%] Fragments - Splitting faces
Info : Writing '/tmp/capacitor_example.xao'...
Info : Done writing '/tmp/capacitor_example.xao'
Info : Clearing all models and views...
Info : Done clearing all models and views
Info : Reading '/tmp/capacitor_example.xao'...
Info : Done reading '/tmp/capacitor_example.xao'
Info : Clearing all models and views...
Info : Done clearing all models and views
Info : [ 0%] Difference
Info : [ 10%] Difference - Performing intersection of shapes
Info : [ 80%] Difference - Building splits of containers
Info : [ 0%] Fragments
Info : [ 10%] Fragments - Performing intersection of shapes
Info : [ 80%] Fragments - Building splits of containers
Info : [ 0%] Difference
Info : [ 10%] Difference
Info : [ 20%] Difference
Info : [ 30%] Difference
Info : [ 40%] Difference
Info : [ 50%] Difference
Info : [ 60%] Difference
Info : [ 70%] Difference
Info : [ 80%] Difference - Splitting faces
Info : [ 0%] Fragments
Info : [ 10%] Fragments
Info : [ 20%] Fragments
Info : [ 30%] Fragments
Info : [ 40%] Fragments
Info : [ 50%] Fragments
Info : [ 60%] Fragments
Info : [ 70%] Fragments
Info : [ 80%] Fragments - Splitting faces
Info : [ 0%] Difference
Info : [ 10%] Difference
Info : [ 20%] Difference
Info : [ 30%] Difference
Info : [ 40%] Difference
Info : [ 50%] Difference
Info : [ 60%] Difference
Info : [ 70%] Difference
Info : [ 80%] Difference - Making faces
Info : [ 90%] Difference - Adding holes
Info : [ 0%] Fragments
Info : [ 10%] Fragments
Info : [ 20%] Fragments
Info : [ 30%] Fragments
Info : [ 40%] Fragments
Info : [ 50%] Fragments
Info : [ 60%] Fragments
Info : [ 70%] Fragments
Info : [ 80%] Fragments - Splitting faces
Info : Writing '/tmp/capacitor_example.xao'...
Info : Done writing '/tmp/capacitor_example.xao'
Info : Clearing all models and views...
Info : Done clearing all models and views
Info : Reading '/tmp/capacitor_example.xao'...
Info : Done reading '/tmp/capacitor_example.xao'
Info : Clearing all models and views...
Info : Done clearing all models and views
Info : [ 0%] Difference
Info : [ 10%] Difference - Performing intersection of shapes
Info : [ 80%] Difference - Building splits of containers
Info : [ 0%] Fragments
Info : [ 10%] Fragments - Performing intersection of shapes
Info : [ 80%] Fragments - Building splits of containers
Info : [ 0%] Difference
Info : [ 10%] Difference
Info : [ 20%] Difference
Info : [ 30%] Difference
Info : [ 40%] Difference
Info : [ 50%] Difference
Info : [ 60%] Difference
Info : [ 70%] Difference
Info : [ 80%] Difference - Splitting faces
Info : [ 0%] Fragments
Info : [ 10%] Fragments
Info : [ 20%] Fragments
Info : [ 30%] Fragments
Info : [ 40%] Fragments
Info : [ 50%] Fragments
Info : [ 60%] Fragments
Info : [ 70%] Fragments
Info : [ 80%] Fragments - Splitting faces
Info : [ 0%] Difference
Info : [ 10%] Difference
Info : [ 20%] Difference
Info : [ 30%] Difference
Info : [ 40%] Difference
Info : [ 50%] Difference
Info : [ 60%] Difference
Info : [ 70%] Difference
Info : [ 80%] Difference - Making faces
Info : [ 90%] Difference - Adding holes
Info : [ 0%] Fragments
Info : [ 10%] Fragments
Info : [ 20%] Fragments
Info : [ 30%] Fragments
Info : [ 40%] Fragments
Info : [ 50%] Fragments
Info : [ 60%] Fragments
Info : [ 70%] Fragments
Info : [ 80%] Fragments - Splitting faces
Info : Writing '/tmp/capacitor_example.xao'...
Info : Done writing '/tmp/capacitor_example.xao'
Info : Clearing all models and views...
Info : Done clearing all models and views
Info : Reading '/tmp/capacitor_example.xao'...
Info : Done reading '/tmp/capacitor_example.xao'
Info : Clearing all models and views...
Info : Done clearing all models and views
Info : [ 0%] Difference
Info : [ 10%] Difference - Performing intersection of shapes
Info : [ 80%] Difference - Building splits of containers
Info : [ 0%] Fragments
Info : [ 10%] Fragments - Performing intersection of shapes
Info : [ 80%] Fragments - Building splits of containers
Info : [ 0%] Difference
Info : [ 10%] Difference
Info : [ 20%] Difference
Info : [ 30%] Difference
Info : [ 40%] Difference
Info : [ 50%] Difference
Info : [ 60%] Difference
Info : [ 70%] Difference
Info : [ 80%] Difference - Splitting faces
Info : [ 0%] Fragments
Info : [ 10%] Fragments
Info : [ 20%] Fragments
Info : [ 30%] Fragments
Info : [ 40%] Fragments
Info : [ 50%] Fragments
Info : [ 60%] Fragments
Info : [ 70%] Fragments
Info : [ 80%] Fragments - Splitting faces
Info : [ 0%] Difference
Info : [ 10%] Difference
Info : [ 20%] Difference
Info : [ 30%] Difference
Info : [ 40%] Difference
Info : [ 50%] Difference
Info : [ 60%] Difference
Info : [ 70%] Difference
Info : [ 80%] Difference - Making faces
Info : [ 90%] Difference - Adding holes
Info : [ 0%] Fragments
Info : [ 10%] Fragments
Info : [ 20%] Fragments
Info : [ 30%] Fragments
Info : [ 40%] Fragments
Info : [ 50%] Fragments
Info : [ 60%] Fragments
Info : [ 70%] Fragments
Info : [ 80%] Fragments - Splitting faces
Info : Writing '/tmp/capacitor_example.xao'...
Info : Done writing '/tmp/capacitor_example.xao'
Info : Clearing all models and views...
Info : Done clearing all models and views
Info : Reading '/tmp/capacitor_example.xao'...
Info : Done reading '/tmp/capacitor_example.xao'
Info : Clearing all models and views...
Info : Done clearing all models and views
Info : [ 0%] Difference
Info : [ 10%] Difference - Performing intersection of shapes
Info : [ 80%] Difference - Building splits of containers
Info : [ 0%] Fragments
Info : [ 10%] Fragments - Performing intersection of shapes
Info : [ 80%] Fragments - Building splits of containers
Info : [ 0%] Difference
Info : [ 10%] Difference
Info : [ 20%] Difference
Info : [ 30%] Difference
Info : [ 40%] Difference
Info : [ 50%] Difference
Info : [ 60%] Difference
Info : [ 70%] Difference
Info : [ 80%] Difference - Splitting faces
Info : [ 0%] Fragments
Info : [ 10%] Fragments
Info : [ 20%] Fragments
Info : [ 30%] Fragments
Info : [ 40%] Fragments
Info : [ 50%] Fragments
Info : [ 60%] Fragments
Info : [ 70%] Fragments
Info : [ 80%] Fragments - Splitting faces
Info : [ 0%] Difference
Info : [ 10%] Difference
Info : [ 20%] Difference
Info : [ 30%] Difference
Info : [ 40%] Difference
Info : [ 50%] Difference
Info : [ 60%] Difference
Info : [ 70%] Difference
Info : [ 80%] Difference - Making faces
Info : [ 90%] Difference - Adding holes
Info : [ 0%] Fragments
Info : [ 10%] Fragments
Info : [ 20%] Fragments
Info : [ 30%] Fragments
Info : [ 40%] Fragments
Info : [ 50%] Fragments
Info : [ 60%] Fragments
Info : [ 70%] Fragments
Info : [ 80%] Fragments - Splitting faces
Info : Writing '/tmp/capacitor_example.xao'...
Info : Done writing '/tmp/capacitor_example.xao'
Info : Clearing all models and views...
Info : Done clearing all models and views
Info : Reading '/tmp/capacitor_example.xao'...
Info : Done reading '/tmp/capacitor_example.xao'
Info : Clearing all models and views...
Info : Done clearing all models and views
Info : [ 0%] Difference
Info : [ 10%] Difference - Performing intersection of shapes
Info : [ 80%] Difference - Building splits of containers
Info : [ 0%] Fragments
Info : [ 10%] Fragments - Performing intersection of shapes
Info : [ 80%] Fragments - Building splits of containers
Info : [ 0%] Difference
Info : [ 10%] Difference
Info : [ 20%] Difference
Info : [ 30%] Difference
Info : [ 40%] Difference
Info : [ 50%] Difference
Info : [ 60%] Difference
Info : [ 70%] Difference
Info : [ 80%] Difference - Splitting faces
Info : [ 0%] Fragments
Info : [ 10%] Fragments
Info : [ 20%] Fragments
Info : [ 30%] Fragments
Info : [ 40%] Fragments
Info : [ 50%] Fragments
Info : [ 60%] Fragments
Info : [ 70%] Fragments
Info : [ 80%] Fragments - Splitting faces
Info : [ 0%] Difference
Info : [ 10%] Difference
Info : [ 20%] Difference
Info : [ 30%] Difference
Info : [ 40%] Difference
Info : [ 50%] Difference
Info : [ 60%] Difference
Info : [ 70%] Difference
Info : [ 80%] Difference - Making faces
Info : [ 90%] Difference - Adding holes
Info : [ 0%] Fragments
Info : [ 10%] Fragments
Info : [ 20%] Fragments
Info : [ 30%] Fragments
Info : [ 40%] Fragments
Info : [ 50%] Fragments
Info : [ 60%] Fragments
Info : [ 70%] Fragments
Info : [ 80%] Fragments - Splitting faces
Info : Writing '/tmp/capacitor_example.xao'...
Info : Done writing '/tmp/capacitor_example.xao'
Info : Clearing all models and views...
Info : Done clearing all models and views
Info : Reading '/tmp/capacitor_example.xao'...
Info : Done reading '/tmp/capacitor_example.xao'
Info : Clearing all models and views...
Info : Done clearing all models and views
Info : [ 0%] Difference
Info : [ 10%] Difference - Performing intersection of shapes
Info : [ 80%] Difference - Building splits of containers
Info : [ 0%] Fragments
Info : [ 10%] Fragments - Performing intersection of shapes
Info : [ 80%] Fragments - Building splits of containers
Info : [ 0%] Difference
Info : [ 10%] Difference
Info : [ 20%] Difference
Info : [ 30%] Difference
Info : [ 40%] Difference
Info : [ 50%] Difference
Info : [ 60%] Difference
Info : [ 70%] Difference
Info : [ 80%] Difference - Splitting faces
Info : [ 0%] Fragments
Info : [ 10%] Fragments
Info : [ 20%] Fragments
Info : [ 30%] Fragments
Info : [ 40%] Fragments
Info : [ 50%] Fragments
Info : [ 60%] Fragments
Info : [ 70%] Fragments
Info : [ 80%] Fragments - Splitting faces
Info : [ 0%] Difference
Info : [ 10%] Difference
Info : [ 20%] Difference
Info : [ 30%] Difference
Info : [ 40%] Difference
Info : [ 50%] Difference
Info : [ 60%] Difference
Info : [ 70%] Difference
Info : [ 80%] Difference - Making faces
Info : [ 90%] Difference - Adding holes
Info : [ 0%] Fragments
Info : [ 10%] Fragments
Info : [ 20%] Fragments
Info : [ 30%] Fragments
Info : [ 40%] Fragments
Info : [ 50%] Fragments
Info : [ 60%] Fragments
Info : [ 70%] Fragments
Info : [ 80%] Fragments - Splitting faces
Info : Writing '/tmp/capacitor_example.xao'...
Info : Done writing '/tmp/capacitor_example.xao'
Info : Clearing all models and views...
Info : Done clearing all models and views
Info : Reading '/tmp/capacitor_example.xao'...
Info : Done reading '/tmp/capacitor_example.xao'
Info : Clearing all models and views...
Info : Done clearing all models and views
Info : [ 0%] Difference
Info : [ 10%] Difference - Performing intersection of shapes
Info : [ 80%] Difference - Building splits of containers
Info : [ 0%] Fragments
Info : [ 10%] Fragments - Performing intersection of shapes
Info : [ 80%] Fragments - Building splits of containers
Info : [ 0%] Difference
Info : [ 10%] Difference
Info : [ 20%] Difference
Info : [ 30%] Difference
Info : [ 40%] Difference
Info : [ 50%] Difference
Info : [ 60%] Difference
Info : [ 70%] Difference
Info : [ 80%] Difference - Splitting faces
Info : [ 0%] Fragments
Info : [ 10%] Fragments
Info : [ 20%] Fragments
Info : [ 30%] Fragments
Info : [ 40%] Fragments
Info : [ 50%] Fragments
Info : [ 60%] Fragments
Info : [ 70%] Fragments
Info : [ 80%] Fragments - Splitting faces
Info : [ 0%] Difference
Info : [ 10%] Difference
Info : [ 20%] Difference
Info : [ 30%] Difference
Info : [ 40%] Difference
Info : [ 50%] Difference
Info : [ 60%] Difference
Info : [ 70%] Difference
Info : [ 80%] Difference - Making faces
Info : [ 90%] Difference - Adding holes
Info : [ 0%] Fragments
Info : [ 10%] Fragments
Info : [ 20%] Fragments
Info : [ 30%] Fragments
Info : [ 40%] Fragments
Info : [ 50%] Fragments
Info : [ 60%] Fragments
Info : [ 70%] Fragments
Info : [ 80%] Fragments - Splitting faces
Info : Writing '/tmp/capacitor_example.xao'...
Info : Done writing '/tmp/capacitor_example.xao'
Info : Clearing all models and views...
Info : Done clearing all models and views
Info : Reading '/tmp/capacitor_example.xao'...
Info : Done reading '/tmp/capacitor_example.xao'
Info : Clearing all models and views...
Info : Done clearing all models and views
Info : [ 0%] Difference
Info : [ 10%] Difference - Performing intersection of shapes
Info : [ 80%] Difference - Building splits of containers
Info : [ 0%] Fragments
Info : [ 10%] Fragments - Performing intersection of shapes
Info : [ 80%] Fragments - Building splits of containers
Info : [ 0%] Difference
Info : [ 10%] Difference
Info : [ 20%] Difference
Info : [ 30%] Difference
Info : [ 40%] Difference
Info : [ 50%] Difference
Info : [ 60%] Difference
Info : [ 70%] Difference
Info : [ 80%] Difference - Splitting faces
Info : [ 0%] Fragments
Info : [ 10%] Fragments
Info : [ 20%] Fragments
Info : [ 30%] Fragments
Info : [ 40%] Fragments
Info : [ 50%] Fragments
Info : [ 60%] Fragments
Info : [ 70%] Fragments
Info : [ 80%] Fragments - Splitting faces
Info : [ 0%] Difference
Info : [ 10%] Difference
Info : [ 20%] Difference
Info : [ 30%] Difference
Info : [ 40%] Difference
Info : [ 50%] Difference
Info : [ 60%] Difference
Info : [ 70%] Difference
Info : [ 80%] Difference - Making faces
Info : [ 90%] Difference - Adding holes
Info : [ 0%] Fragments
Info : [ 10%] Fragments
Info : [ 20%] Fragments
Info : [ 30%] Fragments
Info : [ 40%] Fragments
Info : [ 50%] Fragments
Info : [ 60%] Fragments
Info : [ 70%] Fragments
Info : [ 80%] Fragments - Splitting faces
Info : Writing '/tmp/capacitor_example.xao'...
Info : Done writing '/tmp/capacitor_example.xao'
Info : Clearing all models and views...
Info : Done clearing all models and views
Info : Reading '/tmp/capacitor_example.xao'...
Info : Done reading '/tmp/capacitor_example.xao'
Info : Clearing all models and views...
Info : Done clearing all models and views
Info : [ 0%] Difference
Info : [ 10%] Difference - Performing intersection of shapes
Info : [ 80%] Difference - Building splits of containers
Info : [ 0%] Fragments
Info : [ 10%] Fragments - Performing intersection of shapes
Info : [ 80%] Fragments - Building splits of containers
Info : [ 0%] Difference
Info : [ 10%] Difference
Info : [ 20%] Difference
Info : [ 30%] Difference
Info : [ 40%] Difference
Info : [ 50%] Difference
Info : [ 60%] Difference
Info : [ 70%] Difference
Info : [ 80%] Difference - Splitting faces
Info : [ 0%] Fragments
Info : [ 10%] Fragments
Info : [ 20%] Fragments
Info : [ 30%] Fragments
Info : [ 40%] Fragments
Info : [ 50%] Fragments
Info : [ 60%] Fragments
Info : [ 70%] Fragments
Info : [ 80%] Fragments - Splitting faces
Info : [ 0%] Difference
Info : [ 10%] Difference
Info : [ 20%] Difference
Info : [ 30%] Difference
Info : [ 40%] Difference
Info : [ 50%] Difference
Info : [ 60%] Difference
Info : [ 70%] Difference
Info : [ 80%] Difference - Making faces
Info : [ 90%] Difference - Adding holes
Info : [ 0%] Fragments
Info : [ 10%] Fragments
Info : [ 20%] Fragments
Info : [ 30%] Fragments
Info : [ 40%] Fragments
Info : [ 50%] Fragments
Info : [ 60%] Fragments
Info : [ 70%] Fragments
Info : [ 80%] Fragments - Splitting faces
Info : Writing '/tmp/capacitor_example.xao'...
Info : Done writing '/tmp/capacitor_example.xao'
Info : Clearing all models and views...
Info : Done clearing all models and views
Info : Reading '/tmp/capacitor_example.xao'...
Info : Done reading '/tmp/capacitor_example.xao'
Info : Clearing all models and views...
Info : Done clearing all models and views
Info : [ 0%] Difference
Info : [ 10%] Difference - Performing intersection of shapes
Info : [ 80%] Difference - Building splits of containers
Info : [ 0%] Fragments
Info : [ 10%] Fragments - Performing intersection of shapes
Info : [ 80%] Fragments - Building splits of containers
Info : [ 0%] Difference
Info : [ 10%] Difference
Info : [ 20%] Difference
Info : [ 30%] Difference
Info : [ 40%] Difference
Info : [ 50%] Difference
Info : [ 60%] Difference
Info : [ 70%] Difference
Info : [ 80%] Difference - Splitting faces
Info : [ 0%] Fragments
Info : [ 10%] Fragments
Info : [ 20%] Fragments
Info : [ 30%] Fragments
Info : [ 40%] Fragments
Info : [ 50%] Fragments
Info : [ 60%] Fragments
Info : [ 70%] Fragments
Info : [ 80%] Fragments - Splitting faces
Info : [ 0%] Difference
Info : [ 10%] Difference
Info : [ 20%] Difference
Info : [ 30%] Difference
Info : [ 40%] Difference
Info : [ 50%] Difference
Info : [ 60%] Difference
Info : [ 70%] Difference
Info : [ 80%] Difference - Making faces
Info : [ 90%] Difference - Adding holes
Info : [ 0%] Fragments
Info : [ 10%] Fragments
Info : [ 20%] Fragments
Info : [ 30%] Fragments
Info : [ 40%] Fragments
Info : [ 50%] Fragments
Info : [ 60%] Fragments
Info : [ 70%] Fragments
Info : [ 80%] Fragments - Splitting faces
Info : Writing '/tmp/capacitor_example.xao'...
Info : Done writing '/tmp/capacitor_example.xao'
Info : Clearing all models and views...
Info : Done clearing all models and views
Info : Reading '/tmp/capacitor_example.xao'...
Info : Done reading '/tmp/capacitor_example.xao'
Info : Clearing all models and views...
Info : Done clearing all models and views
Info : [ 0%] Difference
Info : [ 10%] Difference - Performing intersection of shapes
Info : [ 80%] Difference - Building splits of containers
Info : [ 0%] Fragments
Info : [ 10%] Fragments - Performing intersection of shapes
Info : [ 80%] Fragments - Building splits of containers
Info : [ 0%] Difference
Info : [ 10%] Difference
Info : [ 20%] Difference
Info : [ 30%] Difference
Info : [ 40%] Difference
Info : [ 50%] Difference
Info : [ 60%] Difference
Info : [ 70%] Difference
Info : [ 80%] Difference - Splitting faces
Info : [ 0%] Fragments
Info : [ 10%] Fragments
Info : [ 20%] Fragments
Info : [ 30%] Fragments
Info : [ 40%] Fragments
Info : [ 50%] Fragments
Info : [ 60%] Fragments
Info : [ 70%] Fragments
Info : [ 80%] Fragments - Splitting faces
Info : [ 0%] Difference
Info : [ 10%] Difference
Info : [ 20%] Difference
Info : [ 30%] Difference
Info : [ 40%] Difference
Info : [ 50%] Difference
Info : [ 60%] Difference
Info : [ 70%] Difference
Info : [ 80%] Difference - Making faces
Info : [ 90%] Difference - Adding holes
Info : [ 0%] Fragments
Info : [ 10%] Fragments
Info : [ 20%] Fragments
Info : [ 30%] Fragments
Info : [ 40%] Fragments
Info : [ 50%] Fragments
Info : [ 60%] Fragments
Info : [ 70%] Fragments
Info : [ 80%] Fragments - Splitting faces
Info : Writing '/tmp/capacitor_example.xao'...
Info : Done writing '/tmp/capacitor_example.xao'
Info : Clearing all models and views...
Info : Done clearing all models and views
Info : Reading '/tmp/capacitor_example.xao'...
Info : Done reading '/tmp/capacitor_example.xao'
Info : Clearing all models and views...
Info : Done clearing all models and views
Info : [ 0%] Difference
Info : [ 10%] Difference - Performing intersection of shapes
Info : [ 80%] Difference - Building splits of containers
Info : [ 0%] Fragments
Info : [ 10%] Fragments - Performing intersection of shapes
Info : [ 80%] Fragments - Building splits of containers
Info : [ 0%] Difference
Info : [ 10%] Difference
Info : [ 20%] Difference
Info : [ 30%] Difference
Info : [ 40%] Difference
Info : [ 50%] Difference
Info : [ 60%] Difference
Info : [ 70%] Difference
Info : [ 80%] Difference - Splitting faces
Info : [ 0%] Fragments
Info : [ 10%] Fragments
Info : [ 20%] Fragments
Info : [ 30%] Fragments
Info : [ 40%] Fragments
Info : [ 50%] Fragments
Info : [ 60%] Fragments
Info : [ 70%] Fragments
Info : [ 80%] Fragments - Splitting faces
Info : [ 0%] Difference
Info : [ 10%] Difference
Info : [ 20%] Difference
Info : [ 30%] Difference
Info : [ 40%] Difference
Info : [ 50%] Difference
Info : [ 60%] Difference
Info : [ 70%] Difference
Info : [ 80%] Difference - Making faces
Info : [ 90%] Difference - Adding holes
Info : [ 0%] Fragments
Info : [ 10%] Fragments
Info : [ 20%] Fragments
Info : [ 30%] Fragments
Info : [ 40%] Fragments
Info : [ 50%] Fragments
Info : [ 60%] Fragments
Info : [ 70%] Fragments
Info : [ 80%] Fragments - Splitting faces
Info : Writing '/tmp/capacitor_example.xao'...
Info : Done writing '/tmp/capacitor_example.xao'
Info : Clearing all models and views...
Info : Done clearing all models and views
Info : Reading '/tmp/capacitor_example.xao'...
Info : Done reading '/tmp/capacitor_example.xao'
Info : Clearing all models and views...
Info : Done clearing all models and views
Info : [ 0%] Difference
Info : [ 10%] Difference - Performing intersection of shapes
Info : [ 80%] Difference - Building splits of containers
Info : [ 0%] Fragments
Info : [ 10%] Fragments - Performing intersection of shapes
Info : [ 80%] Fragments - Building splits of containers
Info : [ 0%] Difference
Info : [ 10%] Difference
Info : [ 20%] Difference
Info : [ 30%] Difference
Info : [ 40%] Difference
Info : [ 50%] Difference
Info : [ 60%] Difference
Info : [ 70%] Difference
Info : [ 80%] Difference - Splitting faces
Info : [ 0%] Fragments
Info : [ 10%] Fragments
Info : [ 20%] Fragments
Info : [ 30%] Fragments
Info : [ 40%] Fragments
Info : [ 50%] Fragments
Info : [ 60%] Fragments
Info : [ 70%] Fragments
Info : [ 80%] Fragments - Splitting faces
Info : [ 0%] Difference
Info : [ 10%] Difference
Info : [ 20%] Difference
Info : [ 30%] Difference
Info : [ 40%] Difference
Info : [ 50%] Difference
Info : [ 60%] Difference
Info : [ 70%] Difference
Info : [ 80%] Difference - Making faces
Info : [ 90%] Difference - Adding holes
Info : [ 0%] Fragments
Info : [ 10%] Fragments
Info : [ 20%] Fragments
Info : [ 30%] Fragments
Info : [ 40%] Fragments
Info : [ 50%] Fragments
Info : [ 60%] Fragments
Info : [ 70%] Fragments
Info : [ 80%] Fragments - Splitting faces
Info : Writing '/tmp/capacitor_example.xao'...
Info : Done writing '/tmp/capacitor_example.xao'
Info : Clearing all models and views...
Info : Done clearing all models and views
Info : Reading '/tmp/capacitor_example.xao'...
Info : Done reading '/tmp/capacitor_example.xao'
colors = ["tab:blue", "tab:orange", "tab:green"]
for dielectric_epsilon, color in zip([1, 3.9, 16], colors):
plt.plot(
widths,
np.array(Cs_dict[dielectric_epsilon]),
color=color,
linestyle="-",
label=dielectric_epsilon,
)
plt.plot(
widths, np.array(widths) * dielectric_epsilon / separation, color=color, linestyle="--"
)
plt.xlabel("Width / a.u.")
plt.ylabel(r"Capacitance per unit length / $\epsilon_0$ / a.u.")
plt.legend(title="Dielectric")
plt.show()
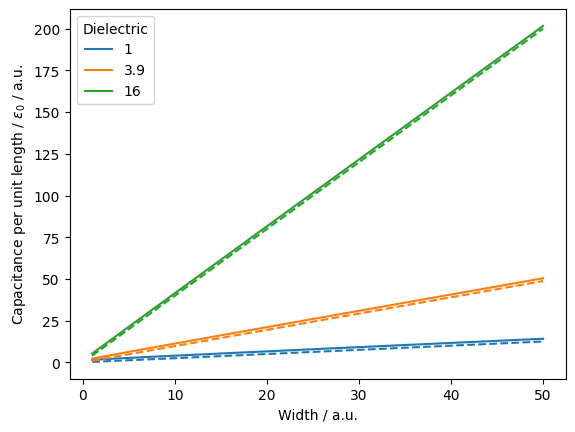
colors = ["tab:blue", "tab:orange", "tab:green"]
for dielectric_epsilon, color in zip([1, 3.9, 16], colors):
reference = np.array(widths) * dielectric_epsilon / separation
plt.plot(
widths,
np.array(Cs_dict[dielectric_epsilon]) / reference,
color=color,
linestyle="-",
label=dielectric_epsilon,
)
plt.xlabel("Width / a.u.")
plt.ylabel(r"Relative error in capacitance per unit length / $\epsilon_0$ / a.u.")
plt.legend(title="Dielectric")
plt.show()
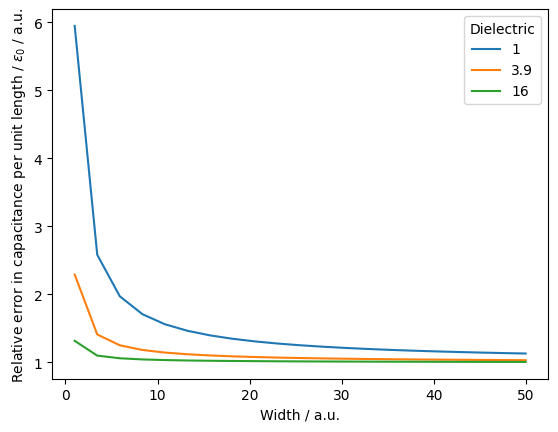
The solver reproduces the parallel-plate capacitor result. For small widths, there is a greater discrepancy between the theoretical parallel plate and the simulated due to the higher relative impact of fringe fields. There is also a constant offset that persists at large widths due to the fringe field contribution. The relative importance of the fringe fields is reduced with increasing dielectric constant which forces more field lines between the two electrodes, as expected.