TiN TOPS heater

Show code cell source Hide code cell source

from collections import OrderedDict

import matplotlib.pyplot as plt
import numpy as np
from shapely.geometry import LineString, Polygon
from skfem import Basis, ElementTriP0
from skfem.io import from_meshio
from tqdm import tqdm

from femwell.maxwell.waveguide import compute_modes
from femwell.mesh import mesh_from_OrderedDict
from femwell.thermal import solve_thermal

In this example we’ll show how to calculate the efficiency of a thermal phase shifter based on calculating the temperature distribution on a 2D plane. I.e. we make the approximation, that the thermal phase shifter is quite long, so that boundary effects will play a negligible role.

We’ll reproduce the TiN TOPS heater presented in [1]. First we set up the mesh:

It consists of a substrate, with a box layer ontop. On the box layer, a waveguide is structured. In this example it’s a silicon waveguide, which has a quite high thermal optical coefficient.

Above the waveguide, within the deposited cladding layer, a TiN resistor is placed for heating up the thermal phase shifter. We refine the mesh within the region of most intered (for very precise results, of course an even finer mesh is required).

w_sim = 8 * 2
h_clad = 2.8
h_box = 2
w_core = 0.5
h_core = 0.22
h_heater = 0.14
w_heater = 2
offset_heater = 2 + (h_core + h_heater) / 2
h_silicon = 0.5

polygons = OrderedDict(
    bottom=LineString(
        [
            (-w_sim / 2, -h_core / 2 - h_box - h_silicon),
            (w_sim / 2, -h_core / 2 - h_box - h_silicon),
        ]
    ),
    core=Polygon(
        [
            (-w_core / 2, -h_core / 2),
            (-w_core / 2, h_core / 2),
            (w_core / 2, h_core / 2),
            (w_core / 2, -h_core / 2),
        ]
    ),
    heater=Polygon(
        [
            (-w_heater / 2, -h_heater / 2 + offset_heater),
            (-w_heater / 2, h_heater / 2 + offset_heater),
            (w_heater / 2, h_heater / 2 + offset_heater),
            (w_heater / 2, -h_heater / 2 + offset_heater),
        ]
    ),
    clad=Polygon(
        [
            (-w_sim / 2, -h_core / 2),
            (-w_sim / 2, -h_core / 2 + h_clad),
            (w_sim / 2, -h_core / 2 + h_clad),
            (w_sim / 2, -h_core / 2),
        ]
    ),
    box=Polygon(
        [
            (-w_sim / 2, -h_core / 2),
            (-w_sim / 2, -h_core / 2 - h_box),
            (w_sim / 2, -h_core / 2 - h_box),
            (w_sim / 2, -h_core / 2),
        ]
    ),
    wafer=Polygon(
        [
            (-w_sim / 2, -h_core / 2 - h_box - h_silicon),
            (-w_sim / 2, -h_core / 2 - h_box),
            (w_sim / 2, -h_core / 2 - h_box),
            (w_sim / 2, -h_core / 2 - h_box - h_silicon),
        ]
    ),
)

resolutions = dict(
    core={"resolution": 0.04, "distance": 1},
    clad={"resolution": 0.6, "distance": 1},
    box={"resolution": 0.6, "distance": 1},
    heater={"resolution": 0.1, "distance": 1},
)

mesh = from_meshio(mesh_from_OrderedDict(polygons, resolutions, default_resolution_max=0.6))
mesh.draw().show()

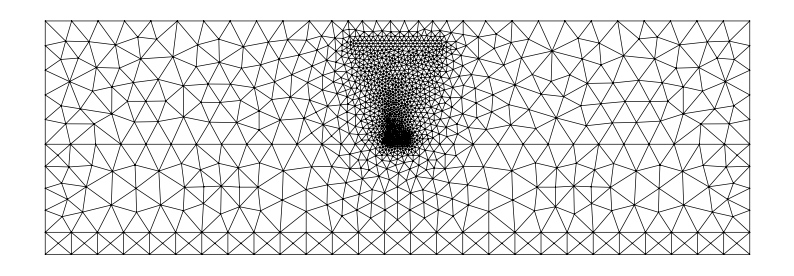
Using the previously defined geometry and the resulting mesh, we can calculate the thermal distribution! For this we start with defining the current densities we want to simulate within the TiN resistor. Here we use the same values as in the referenced paper.

For each temperature distribution we calculate the modes of the waveguide and track their change in effective refractive index. Using the change of the effective refractive index we can calculate the phase shift accumulated within the thermal phase shifter of a given length. To stay consistent with the referenced paper, we use a length of 320um.

currents = np.linspace(0.0, 7.4e-3, 10)
current_densities = currents / polygons["heater"].area
neffs = []

for current_density in tqdm(current_densities):
    basis0 = Basis(mesh, ElementTriP0(), intorder=4)
    thermal_conductivity_p0 = basis0.zeros()
    for domain, value in {
        "core": 90,
        "box": 1.38,
        "clad": 1.38,
        "heater": 28,
        "wafer": 148,
    }.items():
        thermal_conductivity_p0[basis0.get_dofs(elements=domain)] = value
    thermal_conductivity_p0 *= 1e-12  # 1e-12 -> conversion from 1/m^2 -> 1/um^2

    basis, temperature = solve_thermal(
        basis0,
        thermal_conductivity_p0,
        specific_conductivity={"heater": 2.3e6},
        current_densities={"heater": current_density},
        fixed_boundaries={"bottom": 0},
    )

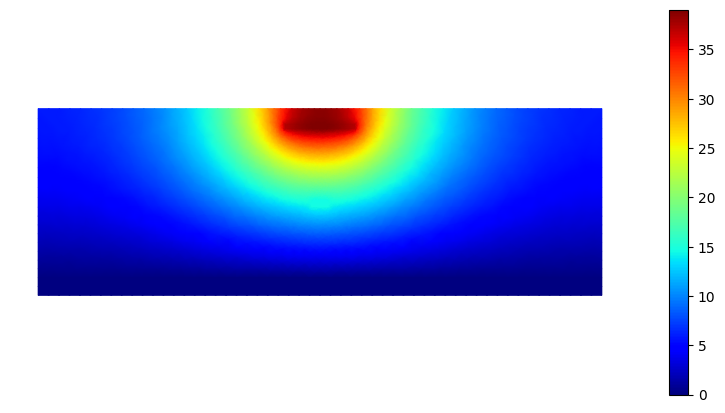
    if current_density == current_densities[-1]:
        basis.plot(temperature, shading="gouraud", colorbar=True)
        plt.show()

    temperature0 = basis0.project(basis.interpolate(temperature))
    epsilon = basis0.zeros() + (1.444 + 1.00e-5 * temperature0) ** 2
    epsilon[basis0.get_dofs(elements="core")] = (
        3.4777 + 1.86e-4 * temperature0[basis0.get_dofs(elements="core")]
    ) ** 2
    # basis0.plot(epsilon, colorbar=True).show()

    modes = compute_modes(basis0, epsilon, wavelength=1.55, num_modes=1)

    if current_density == current_densities[-1]:
        modes[0].show(modes[0].E.real)

    neffs.append(np.real(modes[0].n_eff))

plt.xlabel("Current / mA")
plt.ylabel("Effective refractive index $n_{eff}$")
plt.plot(currents * 1e3, neffs)
plt.show()

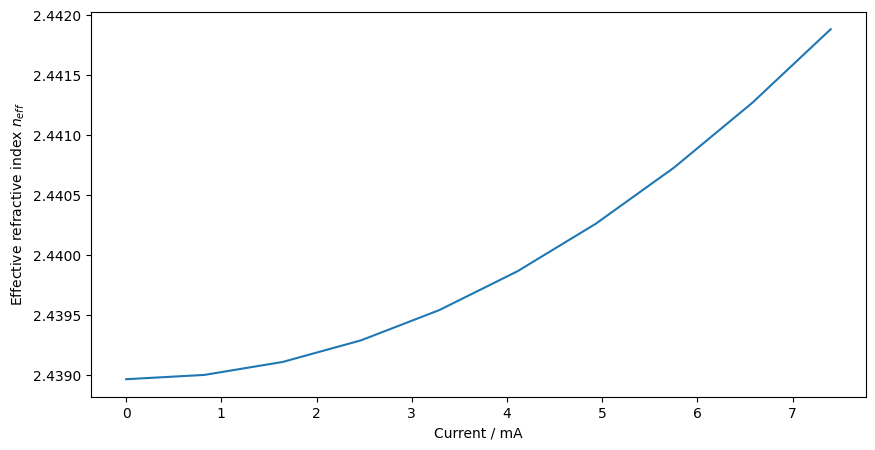
Using the values we calculated for no applied current density and the highest applied current density, we can calculate the phase shift introduced by the current:

print(f"Phase shift: {2 * np.pi / 1.55 * (neffs[-1] - neffs[0]) * 320}")

Phase shift: 3.786321638790277

Bibliography

[1]

Maxime Jacques, Alireza Samani, Eslam El-Fiky, David Patel, Zhenping Xing, and David V. Plant. Optimization of thermo-optic phase-shifter design and mitigation of thermal crosstalk on the SOI platform. Optics Express, 27(8):10456, April 2019. URL: https://doi.org/10.1364/oe.27.010456, doi:10.1364/oe.27.010456.