Selecting modes in the mode solver#
Sometimes we have structures where the mode of interest is not the mode with the highest effective index. There are a few ways to select modes of interest in femwell
Show code cell source
from collections import OrderedDict
import matplotlib.pyplot as plt
import numpy as np
import scipy.constants
from scipy.constants import epsilon_0, speed_of_light
from scipy.integrate import solve_ivp
from shapely.geometry import Polygon
from skfem import Basis, ElementTriP0, Mesh
from skfem.io import from_meshio
from femwell.maxwell.waveguide import compute_modes
from femwell.mesh import mesh_from_OrderedDict
from femwell.utils import inside_bbox
We will use as an example a system with a Si and a SiN sections. This could happen, for example, in a system where we are trying to heat a SiN waveguide with a Si resistor
Show code cell source
w_sim = 6
h_clad = 2
h_box = 2
w_sin = 1
w_si = 0.4
gap = 1.0
h_sin = 0.4
h_si = 0.22
wavelength = 1.55
k0 = 2 * np.pi / wavelength
polygons = OrderedDict(
sin=Polygon(
[
(-w_sin - gap / 2, 0),
(-w_sin - gap / 2, h_sin),
(-gap / 2, h_sin),
(-gap / 2, 0),
]
),
si=Polygon(
[
(w_si + gap / 2, 0),
(w_si + gap / 2, h_si),
(gap / 2, h_si),
(gap / 2, 0),
]
),
clad=Polygon(
[
(-w_sim / 2, 0),
(-w_sim / 2, h_clad),
(w_sim / 2, h_clad),
(w_sim / 2, 0),
]
),
box=Polygon(
[
(-w_sim / 2, 0),
(-w_sim / 2, -h_box),
(w_sim / 2, -h_box),
(w_sim / 2, 0),
]
),
)
resolutions = dict(
sin={"resolution": 0.03, "distance": 1},
si={"resolution": 0.03, "distance": 1},
)
mesh = from_meshio(
mesh_from_OrderedDict(polygons, resolutions, filename="mesh.msh", default_resolution_max=0.2)
)
mesh.draw().show()
basis0 = Basis(mesh, ElementTriP0(), intorder=4)
epsilon = basis0.zeros() + 1.444**2
epsilon[basis0.get_dofs(elements=("si"))] = 3.4777**2
epsilon[basis0.get_dofs(elements=("sin"))] = 1.973**2
0. Directly using femwell#
If we use find_modes, these are the modes we get:
# basis0.plot(epsilon, colorbar=True).show()
modes = compute_modes(basis0, epsilon, wavelength=wavelength, num_modes=4)
for mode in modes:
mode.show("E", part="real")
print(f"The effective index of the SiN mode is {np.real(modes[2].n_eff)}")
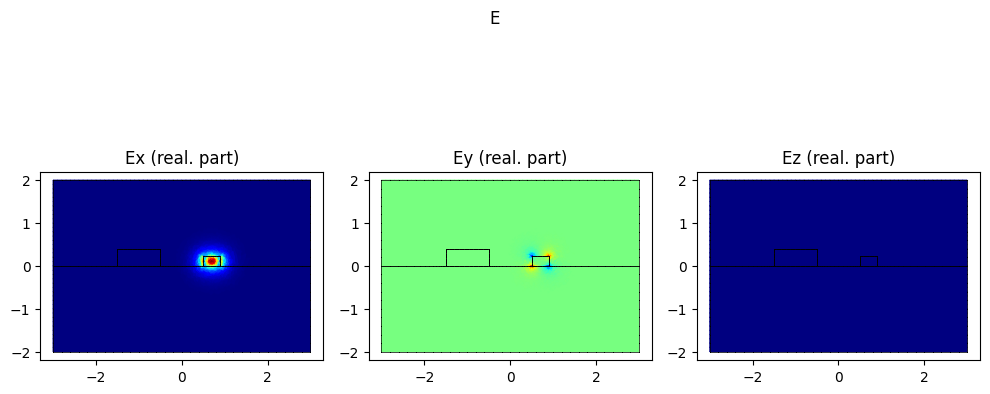
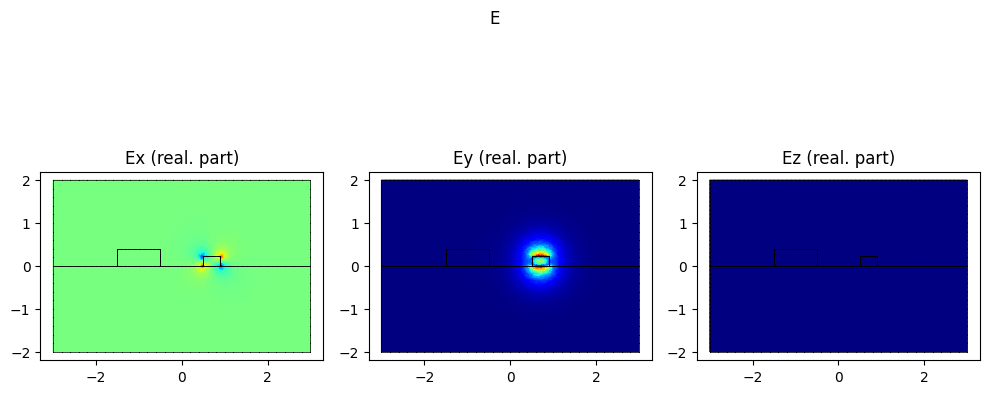
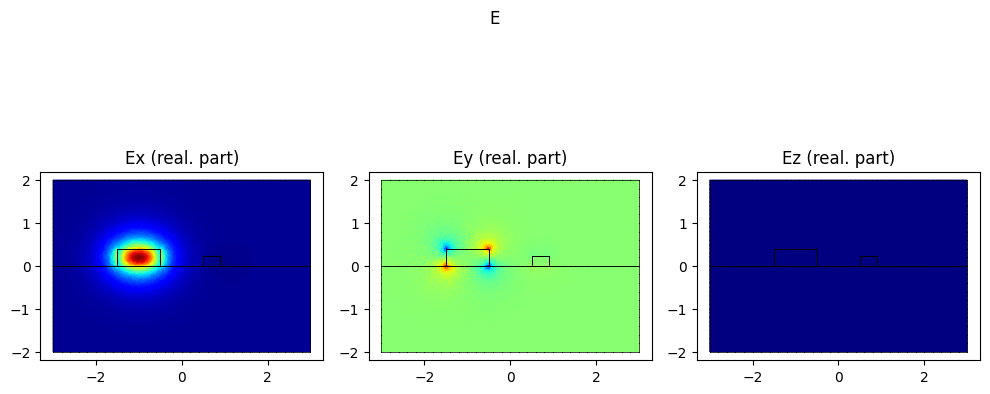
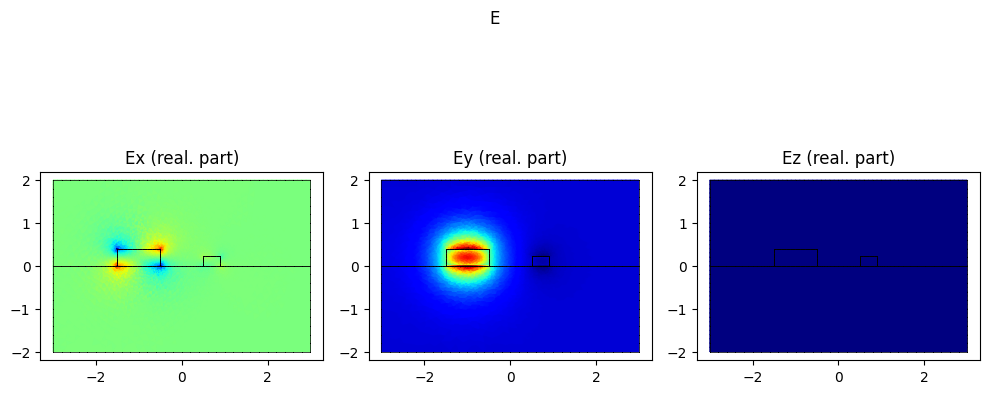
The effective index of the SiN mode is 1.6206394302703988
We can see how to get the SiN mode (which is the mode of interest for us) we need to go to the third mode found by femwell.
Are there easier ways to get the SiN modes? Yes!
1. Hack (not 100% accurate): Erasing the Si waveguide#
One thing we can do to find the SiN mode is to “erase” the Si waveguide, or in other words assign the refractive index of SiO2 to the Si waveguide.
Of course, this is in general not desired, because this way we are missing the effect of the presence of the Si waveguide.
thi smight not be an issue in this example but there’s many examples where this is not an acceptable option.
epsilon = basis0.zeros() + 1.444**2
epsilon[basis0.get_dofs(elements=("si"))] = 1.444**2
epsilon[basis0.get_dofs(elements=("sin"))] = 1.973**2
modes = compute_modes(basis0, epsilon, wavelength=wavelength, num_modes=2)
for mode in modes:
mode.show("E", part="real")
print(f"The effective index of the SiN mode is {np.real(modes[0].n_eff)}")
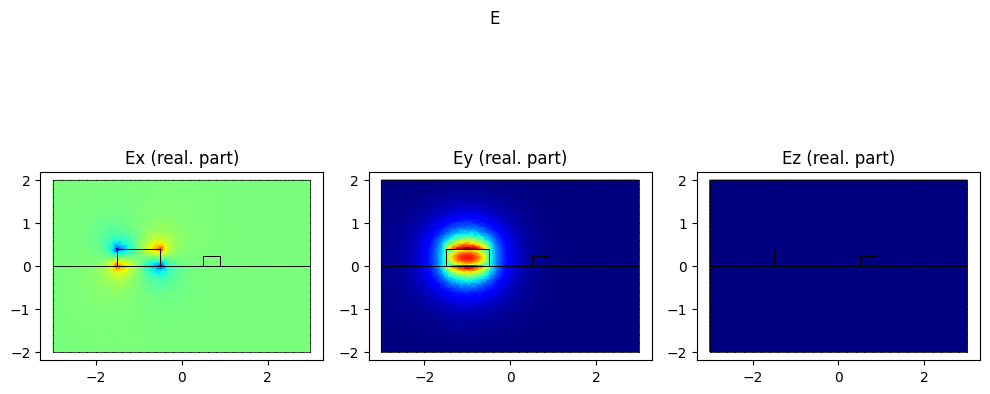
The effective index of the SiN mode is 1.620634697086854
2. Giving a guess effective index#
We can use the n_guess parameter to compute_modes to
select modes close to that effective index.
This is great, but of course we need to know what’s that guess effective index. The way to do that would be to use option 1 above and then use that as the n_guess.
epsilon = basis0.zeros() + 1.444**2
epsilon[basis0.get_dofs(elements=("si"))] = 3.4777**2
epsilon[basis0.get_dofs(elements=("sin"))] = 1.973**2
modes = compute_modes(basis0, epsilon, wavelength=wavelength, num_modes=2, n_guess=1.62)
for mode in modes:
mode.show("E", part="real")
print(f"The effective index of the SiN mode is {np.real(modes[1].n_eff)}")
The effective index of the SiN mode is 1.555952744451575
You can see how using n_guess can still give the wrong mode!
3. Using argsort_modes_by_power_in_elements#
This allows to choose a mode that has the biggest overlap with a given structure.
There are two main ways to specify the structure:
Using the name of the polygon of interest
Giving a square bounding box of coordinates
You can also give it directly the selection_basis of the are of interest.
A requirement for using argsort_modes_by_power_in_elements is to
calculate the H field of the found modes.
modes = compute_modes(basis0, epsilon, wavelength=wavelength, num_modes=4)
# Option 1: using an element name
modes_sorted = modes.sorted(key=lambda mode: -mode.calculate_power(elements="sin").real)
modes_sorted[0].show(modes_sorted[0].E.real, direction="x")
# Option 2: using bounding box
# Format: [xmin, ymin, xmax, ymax]
bbox = [-2, 0, 0, 0.4]
elements = inside_bbox(bbox)
modes_sorted = modes.sorted(key=lambda mode: -mode.calculate_power(elements=elements).real)
modes_sorted[0].show(modes_sorted[0].E.real, direction="x")
/tmp/ipykernel_9712/3937989606.py:7: DeprecationWarning: The behavior of passing an array directly to `show` is deprecated and will be removed in the future. Use `plot` instead.
modes_sorted[0].show(modes_sorted[0].E.real, direction="x")
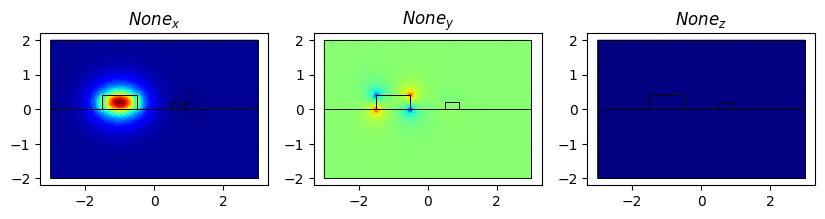
/tmp/ipykernel_9712/3937989606.py:16: DeprecationWarning: The behavior of passing an array directly to `show` is deprecated and will be removed in the future. Use `plot` instead.
modes_sorted[0].show(modes_sorted[0].E.real, direction="x")