Microstrip waveguide - vary gap#
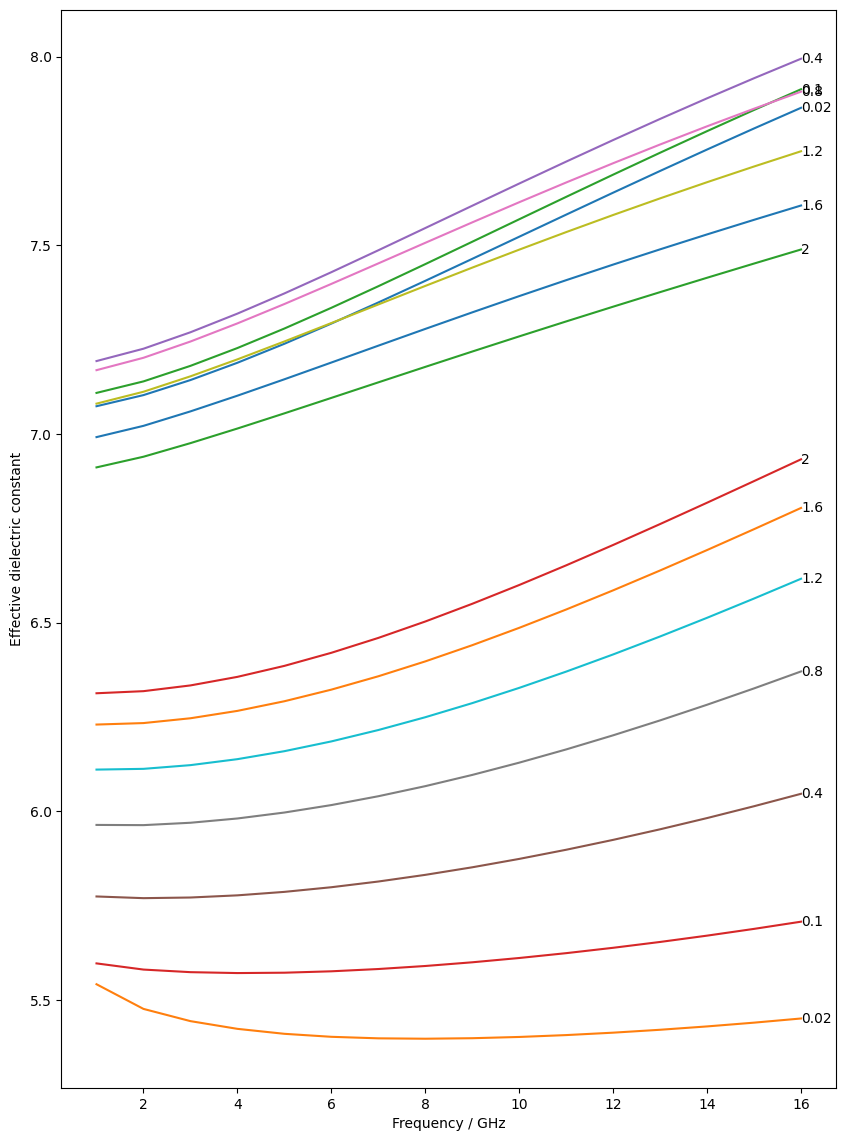
In this example we calculate effective epsilon of the microstrip waveguides from [1]
def mesh_waveguide_1(filename, wsim, hclad, hsi, wcore_1, wcore_2, hcore, gap):
core_l = box(-wcore_1 - gap / 2, -hcore / 2, -gap / 2, hcore / 2)
core_r = box(gap / 2, -hcore / 2, wcore_2 + gap / 2, hcore / 2)
gap_b = box(-gap / 2, -hcore / 2, gap / 2, hcore / 2)
clad = box(-wsim / 2, -hcore / 2, wsim / 2, -hcore / 2 + hclad)
silicon = box(-wsim / 2, -hcore / 2, wsim / 2, -hcore / 2 - hsi)
combined = shapely.ops.unary_union([clad, silicon])
polygons = OrderedDict(
surface=LineString(combined.exterior),
core_l_interface=core_l.exterior,
core_l=core_l,
core_r_interface=core_r.exterior,
core_r=core_r,
gap_b=gap_b,
clad=clad,
silicon=silicon,
)
resolutions = dict(
core_r={"resolution": 0.0024, "distance": 2},
core_l={"resolution": 0.0024, "distance": 2},
core_r_interface={"resolution": 0.0024, "distance": 2, "SizeMax": 1},
core_l_interface={"resolution": 0.0024, "distance": 2, "SizeMax": 1},
# gap_b={"resolution": 0.001, "distance": .01, "SizeMax": .01},
silicon={"resolution": 0.5, "distance": 5},
)
return mesh_from_OrderedDict(
polygons, resolutions, filename=filename, default_resolution_max=10
)
frequencies = np.linspace(1e9, 16e9, 16)
gaps = [0.02, 0.06, 0.1, 0.2, 0.4, 0.6, 0.8, 1, 1.2, 1.4, 1.6, 1.8, 2]
gaps = gaps[::2]
epsilon_effs = np.zeros((len(gaps), len(frequencies), 2), dtype=complex)
for i, gap in enumerate(tqdm(gaps)):
mesh = from_meshio(
mesh_waveguide_1(
filename="mesh.msh",
wsim=30,
hclad=30,
hsi=0.64,
wcore_1=0.6,
wcore_2=0.6,
hcore=0.005,
gap=gap,
)
)
mesh = mesh.scaled((1e-3,) * 2)
for j, frequency in enumerate(tqdm(frequencies, leave=False)):
basis0 = Basis(mesh, ElementTriP0(), intorder=4)
epsilon = basis0.zeros().astype(complex)
epsilon[basis0.get_dofs(elements="silicon")] = 9.9 + 0.0005
epsilon[basis0.get_dofs(elements="clad")] = 1.0
epsilon[basis0.get_dofs(elements="gap_b")] = 1.0
epsilon[basis0.get_dofs(elements="core_l")] = 1 - 1j * 1 / (
18e-6 * 1e-3
) / scipy.constants.epsilon_0 / (2 * np.pi * frequency)
epsilon[basis0.get_dofs(elements="core_r")] = 1 - 1j * 1 / (
18e-6 * 1e-3
) / scipy.constants.epsilon_0 / (2 * np.pi * frequency)
# basis0.plot(np.real(epsilon), colorbar=True).show()
modes = compute_modes(
basis0,
epsilon,
wavelength=scipy.constants.speed_of_light / frequency,
num_modes=2,
metallic_boundaries=True,
)
# print(f"Gap: {gap}, Frequency: {frequency/1e9} GHz")
# print(f"Effective epsilons {modes.n_effs**2}")
# modes[0].show("E", part="real", plot_vectors=True, colorbar=True)
# modes[1].show("E", part="real", plot_vectors=True, colorbar=True)
epsilon_effs[i, j] = modes.n_effs**2
Bibliography#
[1]
R.H. Jansen. High-speed computation of single and coupled microstrip parameters including dispersion, high-order modes, loss and finite strip thickness. IEEE Transactions on Microwave Theory and Techniques, 26(2):75–82, February 1978. URL: http://dx.doi.org/10.1109/TMTT.1978.1129316, doi:10.1109/tmtt.1978.1129316.