from collections import OrderedDict
import matplotlib.pyplot as plt
import numpy as np
import scipy.constants
from shapely.geometry import LineString, Polygon
from skfem import Basis, ElementTriP0, LinearForm
from skfem.io import from_meshio
from tqdm import tqdm
from femwell.maxwell.waveguide import compute_modes
from femwell.mesh import mesh_from_OrderedDict
from femwell.thermal_transient import solve_thermal_transient
# Simulating the TiN TOPS heater in https://doi.org/10.1364/OE.27.010456
w_sim = 8 * 2
h_clad = 2.8
h_box = 1
w_core = 0.5
h_core = 0.22
offset_heater = 2.2
h_heater = 0.14
w_heater = 2
h_silicon = 3
wavelength = 1.55
polygons = OrderedDict(
bottom=LineString([(-w_sim / 2, -h_box), (w_sim / 2, -h_box)]),
core=Polygon(
[
(-w_core / 2, 0),
(-w_core / 2, h_core),
(w_core / 2, h_core),
(w_core / 2, 0),
]
),
heater=Polygon(
[
(-w_heater / 2, offset_heater),
(-w_heater / 2, offset_heater + h_heater),
(w_heater / 2, offset_heater + h_heater),
(w_heater / 2, offset_heater),
]
),
clad=Polygon(
[
(-w_sim / 2, 0),
(-w_sim / 2, h_clad),
(w_sim / 2, h_clad),
(w_sim / 2, 0),
]
),
box=Polygon(
[
(-w_sim / 2, 0),
(-w_sim / 2, -h_box),
(w_sim / 2, -h_box),
(w_sim / 2, 0),
]
),
# silicon=Polygon([
# (-w_sim / 2, - h_box - h_silicon),
# (-w_sim / 2, - h_box),
# (w_sim / 2, - h_box),
# (w_sim / 2, - h_box - h_silicon),
# ]),
)
resolutions = dict(
core={"resolution": 0.05, "distance": 1},
clad={"resolution": 1, "distance": 1},
box={"resolution": 1, "distance": 1},
silicon={"resolution": 1, "distance": 1},
heater={"resolution": 0.05, "distance": 1},
)
mesh = from_meshio(mesh_from_OrderedDict(polygons, resolutions, default_resolution_max=0.3))
basis0 = Basis(mesh, ElementTriP0(), intorder=4)
thermal_conductivity_p0 = basis0.zeros()
for domain, value in {
"core": 148,
"box": 1.38,
"clad": 1.38,
"heater": 28,
}.items(): # , 'silicon': 28
thermal_conductivity_p0[basis0.get_dofs(elements=domain)] = value
thermal_conductivity_p0 *= 1e-12 # 1e-12 -> conversion from 1/m^2 -> 1/um^2
thermal_diffusivity_p0 = basis0.zeros()
for domain, value in {
"heater": 28 / 598 / 5240,
"box": 1.38 / 709 / 2203,
"clad": 1.38 / 709 / 2203,
"core": 148 / 711 / 2330,
# "silicon": 148 / 711 / 2330,
}.items():
thermal_diffusivity_p0[basis0.get_dofs(elements=domain)] = value
thermal_diffusivity_p0 *= 1e12 # 1e-12 -> conversion from m^2 -> um^2
dt = 0.1e-5
steps = 100
def current(t):
return 0.007 / polygons["heater"].area * ((t < dt * steps / 10) + (t > dt * steps / 2))
basis, temperatures = solve_thermal_transient(
basis0,
thermal_conductivity_p0,
thermal_diffusivity_p0,
specific_conductivity={"heater": 2.3e6},
current_densities_0={"heater": current(0)},
current_densities={"heater": current},
fixed_boundaries={"bottom": 0},
dt=dt,
steps=steps,
)
@LinearForm
def unit_load(v, w):
return v
M = unit_load.assemble(basis.with_elements("core"))
times = np.array([dt * i for i in range(steps + 1)])
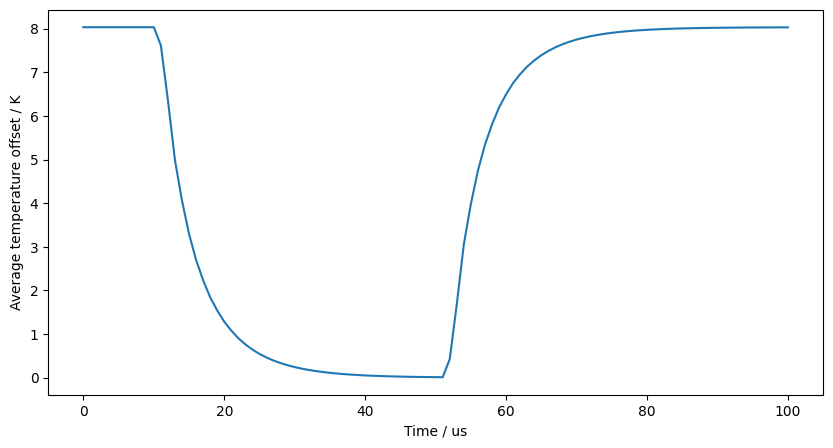
plt.xlabel("Time / us")
plt.ylabel("Average temperature offset / K")
plt.plot(times * 1e6, M @ np.array(temperatures).T / np.sum(M))
plt.show()
# for i in range(0, steps, 10):
# fig, ax = plt.subplots(subplot_kw=dict(aspect=1))
# for subdomain in mesh.subdomains.keys() - {'gmsh:bounding_entities'}:
# mesh.restrict(subdomain).draw(ax=ax, boundaries_only=True)
# basis.plot(temperatures[i], ax=ax, vmin=0, vmax=np.max(temperatures), shading='gouraud')
# plt.show()
# Calculate modes
epsilon_0 = basis0.zeros() + 1.444**2
epsilon_0[basis0.get_dofs(elements="core")] = 3.4777**2
modes_0 = compute_modes(basis0, epsilon_0, wavelength=wavelength, num_modes=1, solver="slepc")
neffs = []
neffs_approximated = []
for temperature in tqdm(temperatures):
# basis.plot(temperature, vmin=0, vmax=np.max(temperatures))
# plt.show()
temperature0 = basis0.project(basis.interpolate(temperature))
epsilon = basis0.zeros() + (1.444 + 1.00e-5 * temperature0) ** 2
epsilon[basis0.get_dofs(elements="core")] = (
3.4777 + 1.86e-4 * temperature0[basis0.get_dofs(elements="core")]
) ** 2
# basis0.plot(epsilon, colorbar=True).show()
modes = compute_modes(basis0, epsilon, wavelength=wavelength, num_modes=1)
# from femwell.mode_solver import plot_mode
# plot_mode(basis_modes, xs[0])
# plt.show()
neffs.append(np.real(modes[0].n_eff))
neffs_approximated.append(np.real(modes_0[0].calculate_pertubated_neff(epsilon - epsilon_0)))
fig = plt.figure()
ax = fig.add_subplot(111)
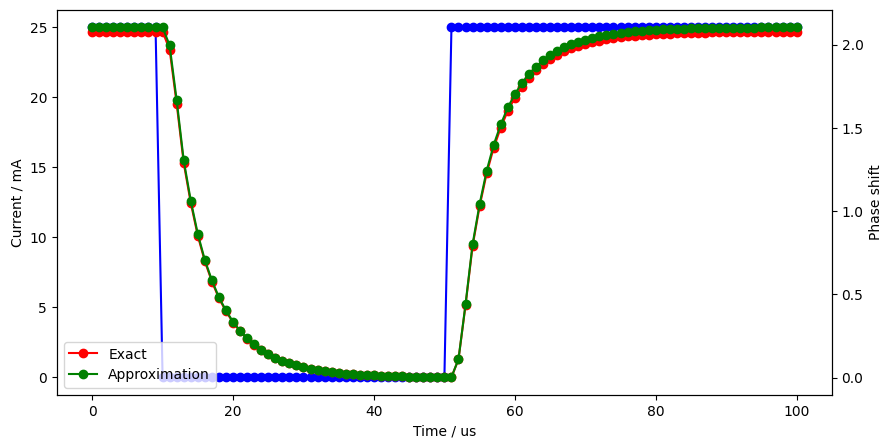
ax.set_xlabel("Time / us")
ax.set_ylabel("Current / mA")
ax.plot(times * 1e6, current(times) * 1000, "b-o")
ax2 = ax.twinx()
ax2.set_ylabel("Phase shift")
ax2.plot(
times * 1e6, 2 * np.pi / wavelength * (neffs - modes_0[0].n_eff) * 320, "r-o", label="Exact"
)
ax2.plot(
times * 1e6,
2 * np.pi / wavelength * (neffs_approximated - modes_0[0].n_eff) * 320,
"g-o",
label="Approximation",
)
plt.legend()
plt.show()