PN junction depletion modulator

Contents

PN junction depletion modulator#

Hide code cell source 
from collections import OrderedDict

import matplotlib.pyplot as plt
import numpy as np
import shapely
from skfem import Basis, ElementTriP0
from skfem.io.meshio import from_meshio

from femwell.maxwell.waveguide import compute_modes
from femwell.mesh import mesh_from_OrderedDict
from femwell.pn_analytical import index_pn_junction, k_to_alpha_dB

/home/runner/miniconda3/lib/python3.12/site-packages/femwell/pn_analytical.py:1: SyntaxWarning: invalid escape sequence '\m'
  """

We can study the propagation constant in waveguides as a function of arbitrary physics. Here, we consider the depletion approximation to pn junctions to study how doping level and junction placement affect modulation in a doped silicon waveguide. This is a simple, yet common, approximation [1].

clad_thickness = 2
slab_width = 3
wg_width = 0.5
wg_thickness = 0.22
slab_thickness = 0.09

core = shapely.geometry.box(-wg_width / 2, -wg_thickness / 2, wg_width / 2, wg_thickness / 2)
slab = shapely.geometry.box(
    -slab_width / 2, -wg_thickness / 2, slab_width / 2, -wg_thickness / 2 + slab_thickness
)
clad = shapely.geometry.box(
    -slab_width / 2, -clad_thickness / 2, slab_width / 2, clad_thickness / 2
)

polygons = OrderedDict(
    core=core,
    slab=slab,
    clad=clad,
)

resolutions = dict(
    core={"resolution": 0.02, "distance": 0.5}, slab={"resolution": 0.04, "distance": 0.5}
)

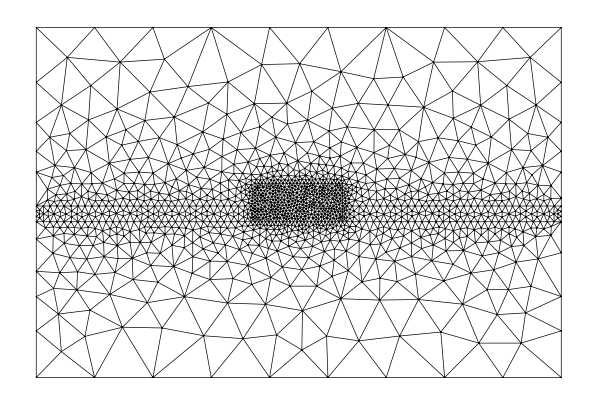
mesh = from_meshio(mesh_from_OrderedDict(polygons, resolutions, default_resolution_max=10))
mesh.draw().show()
../../_images/e9f61ed4307246311e0cfb0fbd7024e4a4ea76f8fac590e4ad52721bbd83b9a2.png

To define the epsilon, we proceed as for a regular waveguide, but we superimpose a voltage-dependent index of refraction based on the Soref Equations [2], [3]. These phenomenologically relate the change in complex index of refraction of silicon as a function of the concentration of free carriers. We model the spatial distribution of carriers according to the physics of a 1D PN junction in the depletion approximation. For more accurate results, full modeling of the silicon processing and physics through TCAD must be performed.

xpn = 0
NA = 1e18
ND = 1e18
V = 0
wavelength = 1.55


def define_index(mesh, V, xpn, NA, ND, wavelength):
    basis0 = Basis(mesh, ElementTriP0())
    epsilon = basis0.zeros(dtype=complex)
    for subdomain, n in {"core": 3.45, "slab": 3.45}.items():
        epsilon[basis0.get_dofs(elements=subdomain)] = n
    epsilon += basis0.project(
        lambda x: index_pn_junction(x[0], xpn, NA, ND, V, wavelength),
        dtype=complex,
    )
    for subdomain, n in {"clad": 1.444}.items():
        epsilon[basis0.get_dofs(elements=subdomain)] = n
    epsilon *= epsilon  # square now
    return basis0, epsilon


basis0, epsilon = define_index(mesh, V, xpn, NA, ND, wavelength)
basis0.plot(epsilon.real, colorbar=True).show()
basis0.plot(epsilon.imag, colorbar=True).show()
../../_images/383e3eb85daf3a3eb40958c52475581d06ad342c735cfbc4fa922e065e8290bd.png ../../_images/1f3dcb8526224a3bf33ac7e1b679ed1078ad2974b69c0add94e7e1ecad00b3c0.png

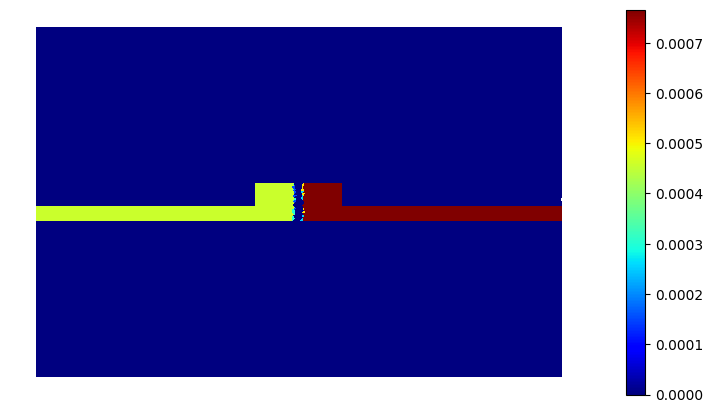
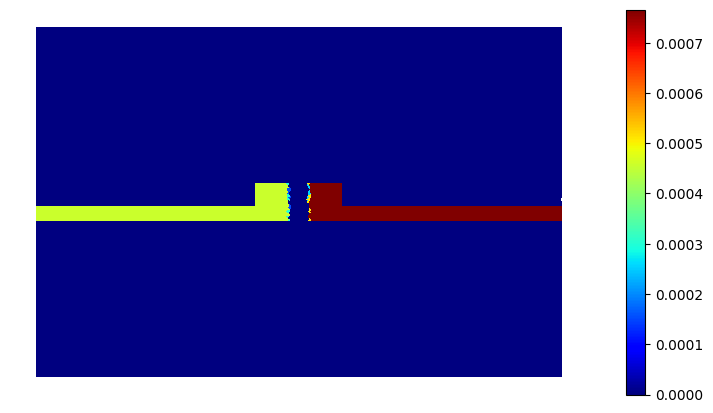
The index change is weak compared to the contrast between silicon and silicon dioxide, but it is accompanied by a change in absorption which is easier to observe. As voltage is increased, the region without charge widens, which is the mechanism behind depletion modulation:

V = -4
basis0, epsilon = define_index(mesh, V, xpn, NA, ND, wavelength)
basis0.plot(epsilon.imag, colorbar=True).show()
../../_images/608ffb029a53fe7eb10544457b6a8fc97e8dc98f8020ce3cbeec78248d45bfa0.png

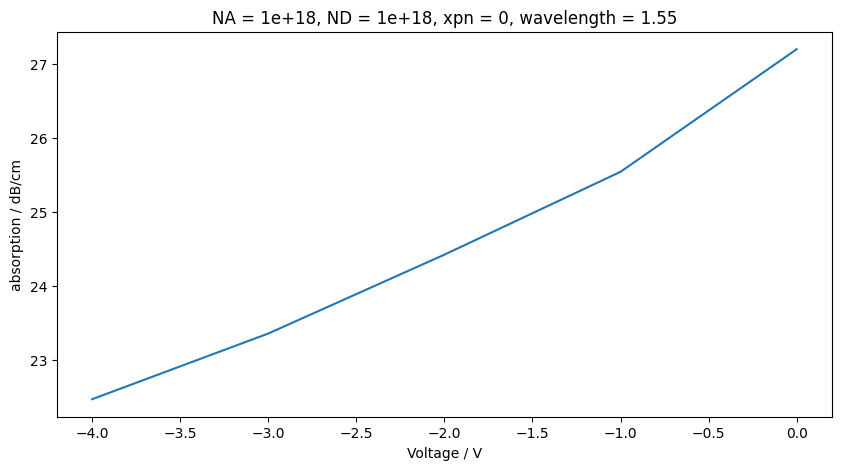
And now we can mode solve as before, and observe the change in effective index and absorption of the fundamental mode as a function of applied voltage for given junction position and doping levels:

voltages = [0, -1, -2, -3, -4]
neff_vs_V = []
for V in voltages:
    basis0, epsilon = define_index(mesh, V, xpn, NA, ND, wavelength)
    modes = compute_modes(basis0, epsilon, wavelength=wavelength, num_modes=1, order=2)
    neff_vs_V.append(modes[0].n_eff)
Hide code cell source 
plt.plot(voltages, np.real(neff_vs_V) - np.real(neff_vs_V[0]))
plt.title(f"NA = {NA}, ND = {ND}, xpn = {xpn}, wavelength = {wavelength}")
plt.xlabel("Voltage / V")
plt.ylabel("Change in neff")
plt.show()
../../_images/974e0ec05ce6e265b6053168697da193acfd4545a6903a9e09243f266f756c40.png
Hide code cell source 
plt.plot(voltages, k_to_alpha_dB(np.imag(neff_vs_V), wavelength))
plt.title(f"NA = {NA}, ND = {ND}, xpn = {xpn}, wavelength = {wavelength}")
plt.xlabel("Voltage / V")
plt.ylabel("absorption / dB/cm")
plt.show()
../../_images/dc4a4235523693728e9b9cd46e7668dc5cd202d23bd8b24166589e499b13ceea.png

Bibliography#

[1]

Lukas Chrostowski and Michael Hochberg. Silicon Photonics Design: From Devices to Systems. Cambridge University Press, Cambridge, England, UK, March 2015. ISBN 978-1-10708545-9. URL: https://doi.org/10.1017/CBO9781316084168, doi:10.1017/CBO9781316084168.

[2]

R. Soref and B. Bennett. Electrooptical effects in silicon. IEEE J. Quantum Electron., 23(1):123–129, January 1987. URL: https://doi.org/10.1109/JQE.1987.1073206, doi:10.1109/JQE.1987.1073206.

[3]

Milos Nedeljkovic, Richard Soref, and Goran Z. Mashanovich. Free-Carrier Electrorefraction and Electroabsorption Modulation Predictions for Silicon Over the 1–14- µm Infrared Wavelength Range. IEEE Photonics J., 3(6):1171–1180, October 2011. URL: https://doi.org/10.1109/JPHOT.2011.2171930, doi:10.1109/JPHOT.2011.2171930.

Contents