Physics-informed propagation loss model

The ability to locally refine the mesh makes FEM well-suited to problems with very different lengthscales.

One such problem is empirically modeling the propagation loss due to sidewall roughness, for instance as performed in [1].

from collections import OrderedDict

import numpy as np
import shapely
from scipy.optimize import curve_fit
from shapely.affinity import scale
from shapely.ops import clip_by_rect
from skfem import Basis, ElementTriP0
from skfem.io.meshio import from_meshio

from femwell.maxwell.waveguide import compute_modes
from femwell.mesh import mesh_from_OrderedDict
from femwell.visualization import plot_domains

Assume there is some information available about TE waveguide loss as a function of wavelength and width:

# Foundry-reported information
wavelengths = (1.55, 1.55)
widths = (0.5, 1)
slab_heights = (0.0, 0.0)
losses = ydata = np.array([2, 1])
core_thickness = 0.22
n_si = 3.45
n_sio2 = 1.44

# Model hyperparameters
sidewall_extent = 0.01

# Format training data
xdata = []
for wavelength, width, slab_height in zip(wavelengths, widths, slab_heights):
    xdata.append((wavelength, width, slab_height))
xdata = np.array(xdata)

Assuming sidewall roughness dominates the loss, we prepare the following mesh:

def waveguide(
    core_width,
    slab_thickness,
    core_thickness=core_thickness,
    slab_width=4,
    sidewall_extent=0.02,
    sidewall_k=1e-4,
    material_k=1e-5,
):
    core = shapely.geometry.box(-core_width / 2, 0, +core_width / 2, core_thickness)

    # Core sidewalls (only keep side extensions)
    core_sidewalls = core.buffer(sidewall_extent, resolution=8)
    core_sidewalls = clip_by_rect(core_sidewalls, -np.inf, 0, np.inf, core_thickness)

    if slab_thickness:
        slab = shapely.geometry.box(-slab_width / 2, 0, +slab_width / 2, slab_thickness)
        waveguide = shapely.union(core, slab)
        clad = scale(waveguide.buffer(5, resolution=8), xfact=0.5)
        polygons = OrderedDict(
            slab=slab,
            core=core,
            core_sidewalls=core_sidewalls,
            clad=clad,
        )
    else:
        clad = scale(core.buffer(5, resolution=8), xfact=0.5)
        polygons = OrderedDict(
            core=core,
            core_sidewalls=core_sidewalls,
            clad=clad,
        )
    resolutions = dict(
        core={"resolution": 0.03, "distance": 0.5},
        core_sidewalls={"resolution": 0.005, "distance": 0.5},
        slab={"resolution": 0.06, "distance": 0.5},
    )

    mesh = from_meshio(mesh_from_OrderedDict(polygons, resolutions, default_resolution_max=10))

    basis0 = Basis(mesh, ElementTriP0())
    epsilon = basis0.zeros(dtype=complex)

    materials = {
        "core": n_si - 1j * material_k,
        "core_sidewalls": n_sio2 - 1j * sidewall_k,
        "clad": n_sio2,
    }

    if slab_thickness:
        materials["slab"] = n_si - 1j * material_k

    for subdomain, n in materials.items():
        epsilon[basis0.get_dofs(elements=subdomain)] = n**2

    return mesh, basis0, epsilon

mesh, basis0, epsilon = waveguide(
    core_width=0.5,
    slab_thickness=0.0,
    core_thickness=0.22,
)

plot_domains(mesh)
basis0.plot(epsilon.real, colorbar=True).show()
basis0.plot(epsilon.imag, colorbar=True).show()

Now that we have a simulation, we can compute TE0 modes, and fit the hyperparameters sidewall_extent and sidewall_index to get a better model for loss as a function of waveguide geometry:

def compute_propagation_loss(
    wavelength,
    core_width,
    slab_thickness,
    core_thickness=core_thickness,
    slab_width=4,
    sidewall_extent=sidewall_extent,
    sidewall_k=1e-4,
    material_k=1e-5,
):
    mesh, basis0, epsilon = waveguide(
        core_width=core_width,
        slab_thickness=slab_thickness,
        core_thickness=core_thickness,
        slab_width=slab_width,
        sidewall_extent=sidewall_extent,
        sidewall_k=sidewall_k,
        material_k=material_k,
    )

    modes = compute_modes(basis0, epsilon, wavelength=wavelength, num_modes=1, order=2)

    keff = modes[0].n_eff.imag
    wavelength_m = wavelength * 1e-6  # convert to m
    alpha = -4 * np.pi * keff / wavelength_m
    return 10 * np.log10(np.exp(1)) * alpha * 1e-2  # convert to cm

for wavelength, core_width, slab_thickness, loss in zip(wavelengths, widths, slab_heights, losses):
    predicted_loss = compute_propagation_loss(
        wavelength=wavelength,
        core_width=core_width,
        slab_thickness=slab_thickness,
        core_thickness=core_thickness,
        slab_width=4,
        sidewall_extent=sidewall_extent,
        sidewall_k=3e-4,
        material_k=2.5e-6,
    )

    print(wavelength, core_width, slab_thickness, predicted_loss, loss)

1.55 0.5 0.0 2.691132834526142 2

1.55 1 0.0 1.109215367294434 1

Pretty close, refine through optimization:

def objective_vector(xdata, sidewall_k, material_k):
    losses_obj = []
    for wavelength, width, slab_height in xdata:
        losses_obj.append(
            compute_propagation_loss(
                wavelength=wavelength,
                core_width=width,
                slab_thickness=slab_height,
                core_thickness=core_thickness,
                slab_width=4,
                sidewall_extent=sidewall_extent,
                sidewall_k=sidewall_k,
                material_k=material_k,
            )
        )
    return losses_obj

popt, pcov = curve_fit(objective_vector, xdata, ydata, bounds=(0, [1e-2, 1e-2]), p0=(3e-4, 1e-6))

/tmp/ipykernel_9175/51164132.py:1: OptimizeWarning: Covariance of the parameters could not be estimated
  popt, pcov = curve_fit(objective_vector, xdata, ydata, bounds=(0, [1e-2, 1e-2]), p0=(3e-4, 1e-6))

popt, pcov

(array([1.86930725e-04, 2.42089660e-06]),
 array([[inf, inf],
        [inf, inf]]))

for wavelength, core_width, slab_thickness, loss in zip(wavelengths, widths, slab_heights, losses):
    predicted_loss = compute_propagation_loss(
        wavelength=wavelength,
        core_width=core_width,
        slab_thickness=slab_thickness,
        core_thickness=core_thickness,
        slab_width=4,
        sidewall_extent=sidewall_extent,
        sidewall_k=popt[0],
        material_k=popt[1],
    )

    print(wavelength, core_width, slab_thickness, predicted_loss, loss)

1.55 0.5 0.0 2.000000000391118 2

1.55 1 0.0 0.9999999998027127 1

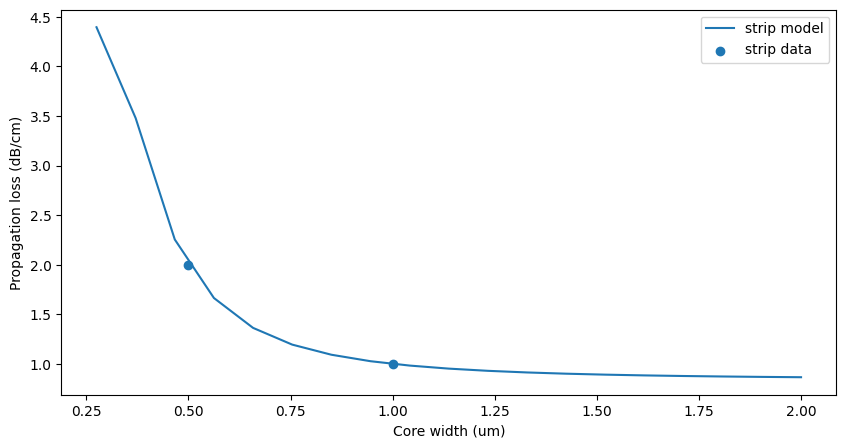
widths_plot = np.linspace(0.275, 2.0, 19)
losses_plot_strip = []
for width in widths_plot:
    losses_plot_strip.append(
        compute_propagation_loss(
            wavelength=1.55,
            core_width=width,
            slab_thickness=0.0,
            core_thickness=core_thickness,
            slab_width=4,
            sidewall_extent=sidewall_extent,
            sidewall_k=popt[0],
            material_k=popt[1],
        )
    )

import matplotlib.pyplot as plt

plt.plot(widths_plot, losses_plot_strip, label="strip model")
plt.scatter(widths, losses, label="strip data")

plt.legend()
plt.xlabel("Core width (um)")
plt.ylabel("Propagation loss (dB/cm)")

Text(0, 0.5, 'Propagation loss (dB/cm)')

Bibliography

[1]

Susan M. Lindecrantz and Olav Gaute Hellesø. Estimation of propagation losses for narrow strip and rib waveguides. IEEE Photonics Technology Letters, 26(18):1836–1839, 2014. doi:10.1109/LPT.2014.2337055.